Gelingt der große Wurf?

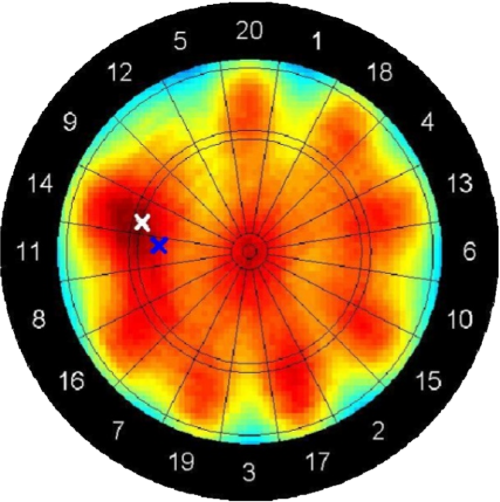
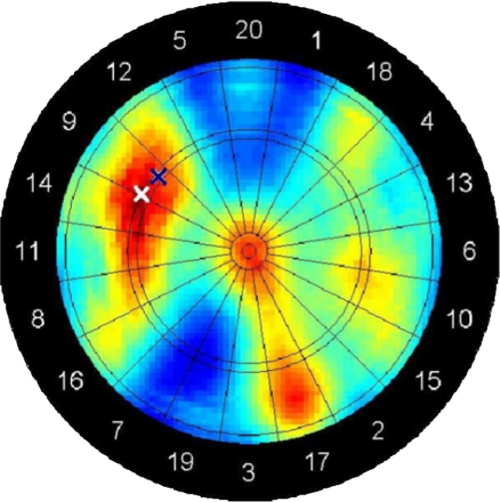
Ein weiterer interessanter Punkt, der Raum für vielfältige Untersuchungen bietet ist die Frage, wie ein optimaler Zielpunkt zu wählen ist, wenn es um das Erreichen einer bestimmten Punktzahl mit mehreren Würfen geht. Auf Details des Modells wird an dieser Stelle verzichtet, es soll lediglich ein Beispiel angegeben werden, welches auf der im vorherigen Abschnitt gezeigten Trefferverteilung und den davon abhängigen optimalen Zielpunkten basiert. Möchte man z.B. mit den 3 Würfen einer Runde 53 Punkte erzielen, so wird als erstes Ziel (weißes Kreuz) ein Punkt am Rande der Triple-14 empfohlen, die Erfolgswahrscheinlichkeit für das Gesamtziel 53 Punkte zu 32.5% berechnet (siehe Abb. 9, oben). Erzielt der Spieler nun eine 11 (blaues Kreuz), so bleiben 42 Punkte in 2 Würfen zu erreichen. Jetzt wird als Ziel der Rand der Triple-9 ausgegeben (siehe Abb. 9, unten), Erfolgswahrscheinlichkeit: 19%. Trifft der Spieler eine Triple-9 (blaues Kreuz), so bleiben 15 Punkte für den letzten Wurf und die Erfolgchancen hierfür steigen auf 45.1%.

Abbildung 9: Zielpunkte bei einer Serie von 3 Würfen

Das Konzept zur Behandlung von Wurfserien kann sogar noch ausgebaut werden: Abhängig vom momentanen Spielstand kann man sich fragen, welcher Zielpunkt mit der größten Wahrscheinlichkeit zum Gewinn des gesamten Spiels führt. Um hier gute Aussagen zu bekommen, ist allerdings eine realistische Prognose über die vom Gegner in der nächsten Runde erzielten Punkte erforderlich. Eine sehr elegante Lösungsmöglichkeit ergibt sich durch eine rekursive Berechnung dieser Gewinnwahrscheinlichkeit:
Man ermittelt zunächst für Spielstände nahe dem Spielende
(0:1, 0:2, 0:3,. . . ,1:0,2:0,3:0,. . . ,1:1, 1:2, 1:3,. . . ) den Wert, was leicht mit den bereits behandelten Methoden möglich ist. Hat man komplexere Spielstände, wie z.B. 15:27, so kann mit dem Konzept der bedingten Wahrscheinlichkeit aus der Gewinnwahrscheinlichkeit eines bereits berücksichtigen Spielstandes und der Wahrscheinlichkeit für das Erreichen dieses Spielstandes die entsprechende Gewinnchance auch für den komplexen Spielstand bestimmen. Wenn sich die Trefferbilder der Spieler nicht ändern, kann man die zeitintensive rekursive Berechnung sogar online vornehmen und dann während des Spiels sehr schnell günstige Zielpunkte angeben.

5 Mögliche Erweiterungen

Die bisher beschriebenen Ansätze können im Grunde beliebig ausgebaut werden. Eine Idee wäre dabei, zusätzlich zu den beschriebenen Methoden, die eine Berechnung der Gewinnwahrscheinlichkeit abhängig vom momentanen Spielstand erlauben, die momentane Spielstärke beider Spieler zu berücksichtigen. Dies würde bedeuten, dass die Ergebnisse beider Spieler ständig aufgezeichnet werden, nach Möglichkeit unter zusätzlicher Angabe des jeweils gewählten Zielpunktes (den man für den Gegner natürlich in der Regel nicht kennt).

Mit diesen Informationen könnte die Trefferverteilung der Spieler laufend während des Spiels angepasst werden und somit auch Formschwankungen oder äußere Einflüsse in der Spielsituation berücksichtigt werden. Für die Prognose der Ergebnisse des Gegners kann man entweder davon ausgehen, dass dieser mit derselben, in gewissem Maße also optimalen Strategie spielt; eine andere Möglichkeit wäre, aus den Treffern des Gegners und dem zugehörigen Spielstand zu versuchen, auf seine Spielstrategie und -stärke zu schließen und anschließend Vorhersagen über seine zukünftigen Ergebnisse zu erlangen. Eine weitere interessante Aufgabe wäre die, bei Beobachtung des Spiels zweier Spieler möglichst realistische Prognosen für den Ausgang eines Duells abzugeben - also sozusagen Wettquoten zu ermitteln!

Trotz fehlender Details der gerade vorgeschlagenen Erweiterungen wird deutlich, dass das vorgestellte Projekt sehr viel Raum auch für wissenschaftliche Untersuchungen bis hin zur Diplomarbeit bietet. Gleichzeitig sind aber auch schon mit sehr begrenzten mathematischen Hilfsmitteln Ergebnisse zu erzielen, die einen wertvollen Beitrag zur Beantwortung der ursprünglichen Fragestellung liefern. Die in jedem Fall bleibenden offenen Fragen - sei es aus Mangel an Zeit oder aufgrund fehlender Kenntnisse - liefern dem Leser hoffentlich die Motivation, sich weiter mit der Bearbeitung ähnlicher Projekte und dem Vertiefen der eigenen mathematischen Fähigkeiten zu befassen.