Gelingt der große Wurf?

3 Der Computer spielt Darts

Eine Möglichkeit, die Auswirkungen verschiedener Zielpunkte zu vergleichen, wäre, einfach sehr viele Testreihen durchzuführen, wobei sich jeweils bei fester Anzahl N von Würfen (z.B. 100) der Punkt, auf den gezielt wird, ändert. Da dieser Versuch im Grunde von einem Spieler ausgeführt werden muss, stellt sich schnell eine Ermüdung ein. Wo liegen überhaupt aussichtsreiche Kandidaten für gute Zielpunkte? Wie viele solcher Testreihen müssen durchgeführt werden, damit man eine halbwegs brauchbare Aussage treffen kann? Und kann man ein auf diese Weise erzieltes Ergebnis überhaupt auf andere Spieler übertragen, oder müssten diese ebenfalls eine große Anzahl von Versuchen hinter sich bringen?

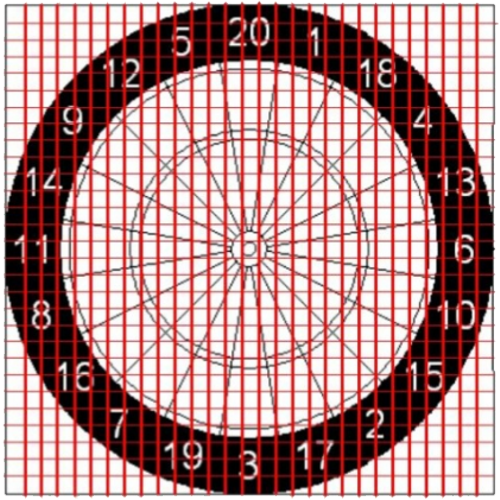
Abbildung 3: Rasterung der Dartscheibe, Rasterweite 5mm

An dieser Stelle können wir dem Computer einen Großteil der Arbeit übertragen. Im Zentrum steht dabei die Annahme, dass ein Trefferbild wie in Abbildung 2, welches ja einem bestimmten Zielpunkt zugeordnet ist, sich bei Änderung dieses Zielpunktes nicht grundlegend ändert. Vereinfachend kann man zunächst sogar davon ausgehen, dass sich für jeden möglichen Zielpunkt dasselbe Trefferbild ergibt (diese Annahme wird später bei Bedarf abgeschwächt werden).

Nun ist es selbst ohne Kenntnisse stochastischer Methoden möglich, auf Basis einer ermittelten Trefferverteilung, bei der z.B. der Scheibenmittelpunkt als Zielpunkt gewählt wurde, durchschnittlich erzielte Punktzahlen auch für andere Ziele zu berechnen: Wenn die N Koordinaten der Treffer aus dem Experiment ermittelt wurden, werden diese Koordinaten einfach relativ zu einem Zielpunkt
Z = (x₀; y₀) ≠ (0; 0) betrachtet und damit ein Trefferbild für diesen neuen Zielpunkt generiert, für das leicht die im Durchschnitt pro Wurf erzielte Punktzahl berechnet werden kann.

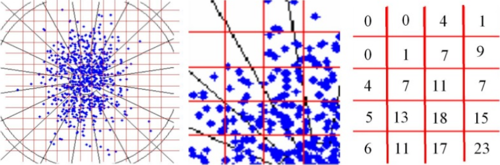
Abbildung 4: Übertragung der Trefferverteilung in ein Raster

Dieses Prinzip kann der Computer bei geeigneter Programmierung für eine große Zahl möglicher Zielpunkte vornehmen; so kann beispielsweise die ganze Dartscheibe mit einem Raster der Weite 1mm überdeckt (vgl. Abb. 3, hier: Rasterweite 5mm) und jeder Rasterpunkt als potentieller Zielpunkt untersucht werden (vgl. Abb. 5).

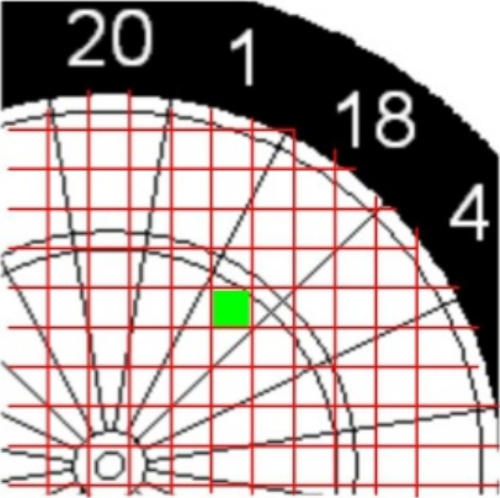
Abbildung 5: Verschiebung der gerasterten Trefferverteilung in neuen Zielpunkt

>> Zielpunkte zur Erzielung der maximalen Punktzahl