Zwei Arten motorischer Strategien
für einen genauen Dartwurf
Die vorliegende wissenschaftliche Arbeit stellt eine wertvolle Ergänzung unserer Artikel zur Verbesserung der Technik im Dartsport dar. Vielen Dank an Daiki Nasu von der Universität Osaka, der eine Veröffentlichung auf Darts1 möglich machte.
Zusammenfassung
Diese Studie untersucht, ob erfahrene Dartspieler bestimmte Muster im Bewegungsablauf ihrer Hand nutzen, um die zwangsweisen Schwankungen im Abwurf-Timing zu kompensieren. Acht erfahrene Spieler und acht Anfänger führten jeweils 60 Dartswürfe aus, bei denen sie auf das Bullseye zielten. Die Bewegung der Darts und des Zeigefingers wurden mit sieben 480-Hertz-Kameras aufgezeichnet. Die Daten wurden unter Verwendung einer kubischen Spline-Funktion interpoliert und auf die Millisekunde genau analysiert. Die erwarteten vertikalen Fehler auf der Dartscheibe wurden auf Grundlage der Zustandsgrößen des Zeigefingers (Position, Geschwindigkeit und Richtung der Bewegung) in einer Zeitreihe berechnet. Diese Zeitreihen-Fehler bilden die Bewegungsmuster der Hand ab. Für die Bewertung auf Basis der Zeitreihen-Fehler wurden zwei Variablen für die vertikale Ebene und zwei Variablen bezüglich der Kontrolle des Timings vergeben. Die Ergebnisse zeigten in der Gruppe der erfahrenen Spieler zwei typische Arten von Bewegungsabläufen. Die Timing-Fehler der erfahrenen Spieler entsprachen denen der Anfänger, jedoch hatten die erfahrenen Spieler ein größeres Zeitfenster, um einen Dart genau abzuwerfen. Diese Probanten wählten bestimmte Bewegungsmuster ihrer Hand, um die Timing-Fehler zu kompensieren. Andere erfahrene Spieler wählten nicht die ergänzenden Bewegungsabläufe der Hand, aber sie reduzierten stark ihre Fehler beim Abwurf-Timing.
Einführung
Ein genauer Wurf ist seit der Steinzeit bis zum heutigen Sportzeitalter eine wichtige Fähigkeit. Für die Jäger der Steinzeit mag ein exakter Wurf Voraussetzung gewesen sein, um Beute auf große Entfernung jagen zu können. Für Baseball-, Basketball- oder Darts-Spieler hat ein genauer Wurf oder Schuss größten Einfluss auf das Resultat des Spieles. In der vorliegenden Studie untersuchten wir den Dartwurf als typisches Beispiel für einen exakten Wurf. Welche Bewegungsabläufe benötigt man für einen exakten Wurf?
Der Treffpunkt des Darts auf der Scheibe ist von einer Kombination aus physischen Faktoren abhängig, inklusive der Position, Geschwindigkeit und der Bewegungsrichtung zum Zeitpunkt des Abwurfes. Die Rotation des Darts und den Luftwiderstand haben wir bei der Untersuchung vernachlässigt. Diese Parameter sind abhängig von der Bewegungskurve der Wurfhand und des Abwurf-Zeitpunktes. Um die Schwankungsbreite bei wiederholten Würfen zu reduzieren, ist es wichtig, dass der Spieler sowohl die Schwankungsbreite der Bewegungskurve der Hand als auch des Abwurf-Timings reduziert.
Mehrere Studien haben gezeigt, dass eine Kontrolle des exakten Abwurf-Zeitpunktes der wichtigste Faktor für einen genauen Wurf ist. Hore und andere berichteten [1],[2], dass die Genauigkeit beim Überkopfwurf eines Balles nicht mit der genauen Handbewegung einherging, sondern vielmehr der Präzision des Timings, gemessen zum Zeitpunkt der vertikalen Position der Hand im Raum. Hore und andere erklärten [3], dass Werfer beim Baseball (Pitcher) eine Abwurf-Genauigkeit von einer bis zwei Millisekunden erwischen mussten, um regelmäßig die Strike-Zone zu treffen. Was Darts angeht, so darf der Zeitpunkt des Abwurfes theoretisch maximal 1,8 Millisekunden vom Ideal abweichen, um das Bullseye mit einem Durchmesser von 4,4 Zentimetern treffen zu können. Weitere Studien haben ergeben, dass Werfer ein maximales Zeitfenster von 1 Millisekunde haben, um ein Ziel mit einem Durchmesser von 20 Zentimetern zu treffen, wenn es weiter als sechs Meter entfernt ist. [5],[6].
Auf der anderen Seite sagen Newell und Corcos [7], dass "Schwankungen bei und zwischen allen biologischen Systemen von Natur aus gegeben sind." Es wurde zu Grunde gelegt, dass Schwankungen im Experiment beim menschlichen Verhalten auftreten, weil auf allen Niveaus des Nervensystems Rauschen auftritt (z.B. synaptisch, neural und muskuläre Störungen) [8]. Auf dieser Voraussetzung basierend wäre es überraschend, wenn das zentrale Nervensystem in der Lage wäre, den Abwurfzeitpunkt innerhalb von 1 bis 2 Millisekunden bei jedem Wurf kontrollieren zu können. Tatsächlich, Verhaltensstudien berichten von einer stärkeren Schwankungsbreite im Timing als die theoretisch zulässige Größenordnung zulassen würde. (z.B. 9 ms bei einer virtuellen Wurfaufgabe [9], 7–10 ms für Ballwürfe von Freizeitspielern [1],[2],[10], und 27 ms für den Ballwurf von unerfahrenen Probanten [11]).
Zwei frühere Studien legten nahe, dass die Variabilität des Timings durch eine Modifikation der Bewegungsbahn der Hand kompensiert werden kann. Müller and Loosch [12] demonstrierten, dass Werfer Bewegungsmuster entwickelten, die das Zeitfenster des Abwurfes für ein genaues Ergebnis in einer virtuellen Eingelenk Wurfaufgabe maximierten. Das bedeutet, das Werfer Bewegungsmuster lernten, die die Empfindlichkeit für Timing Fehler reduzieren könnten, welche ohne präzise Kontrolle des Timings zum Erfolg führten. Cohen und Sternad [9] entwickelten Müller's Studie weiter und lieferten Beweise für ihre Behauptungen. Sie berichteten, dass die Werfer bei einer virtuellen Wurfaufgabe genaues Timing lernten und ihre Leistung steigern konnten, aber sie erreichten bei der Steigerung ein Plateau. Auf lange Sicht optimierten die Werfer in der Studie beim zusätzlichen Training die Bewegungsmuster ihrer Hand, um die anlagebedingten Beschränkungen im Timing des Abwurfes zu kompensieren. Allerdings scheint es verfrüht, ihre Ergebnisse für den allgemeinen Fall zu akzeptieren, da die virtuelle Wurfaufgabe in der genannten Studie beschränkter und spezifischer war als eine reale Wurfaufgabe.
Smeets et al. [4] präsentierten experimentelle Daten und Simulationen für tatsächliches Dartwerfen und fanden Ergebnisse, die im Widerspruch zu den von Müller’s [12] und Cohen’s [9] Studien stehen. Durch Training reduzierten die Probanden die Radien ihrer Bewegungsbahn der Hand und ihr Abwurfpunkt veränderte sich, annähernd dem Scheitelpunkt ihrer Handbewegung. Diese Veränderungen verringerten nicht die Empfindlichkeit für Fehler beim Timing des Abwurfes, das Gegenteil war der Fall. Lediglich vier Probanden nahmen an der Studie von Smeets teil. Ihre Erfahrung als Dartspieler reichten laut ihren Angaben von "einige Male im Monat" bis "überhaupt erst ein paar Mal". Die Probanden der erwähnten Studie könnten eine Stufe vor dem Erlernen der Muster für Bewegungsabläufe der Hand gestanden haben, die die Anfälligkeit für Fehler beim Timing reduzieren können.
Weil, wie oben erwähnt, die Unbeständigkeit beim Timing nicht vollständig beseitigt werden kann, sollten fortgeschrittene Dartspieler diejenige Handbewegung ausführen, die die Unbeständigkeit beim Timing am besten kompensiert. Die aktuelle Studie untersucht, ob fortgeschrittene Dartspieler einen Bewegungsablauf der Hand nutzen, um die innewohnende Unbeständigkeit beim Abwurf Timing auszugleichen. Wir haben mehrere Hypothesen überprüft, indem wir erfahrene Spieler und Anfänger verglichen. In verschiedenen Aufgaben den Wurf betreffend, wurde berichtet, dass durch Training die Unbeständigkeit in der Bewegung reduziert wurde. Zum Beispiel in der gemeinsamen Bewegungslehre [13],[14], Eckdaten des Abwurfes [15]–[17] und des Abwurf-Timings [9].
Deshalb sagten wir voraus, dass erfahrene Spieler eine geringere Unbeständigkeit beim Abwurf Timing aufweisen würden als Anfänger. Es ist jedoch unwahrscheinlich, dass Werfer einen Abwurf Zeitpunkt innerhalb 1 ms kontrollieren können. Folgende Hypothesen wurden in dieser Studie untersucht: 1) Erfahrene Spieler zeigen kleinere Abweichungen im Timing als Anfänger, jedoch nicht in der Größenordnung von 1 ms. 2) Erfahrene Spieler haben durch Training ergänzende Muster ihrer Handbewegung gelernt, die Unbeständigkeiten beim Timing ausgleichen. Weil die horizontale Handbewegung nahezu perfekt in einer Linie mit dem anvisierten Ziel liegt, beeinflusst dies kaum die Ungenauigkeit in der Horizontalen. [4],[12]. Daher konzentrierten wir uns nur auf die Bewegung und die Ergebnisse in der vertikalen Ebene.
Materialien und Methoden
Testpersonen
Ein Experiment wurde mit 16 Männern durchgeführt. Die Expertengruppe bestand aus acht Rechtshändern im Alter zwischen 25 und 49 Jahren. Es waren turniererfahrene E-Dart Spieler, die seit zwei bis sechs Jahren Darts spielten. Die übrigen acht Rechtshänder (Studenten und Lehrkörper) bildeten die Gruppe der Anfänger. Sie waren zwischen 19 und 37 Jahre alt. Jeder der Anfänger hatte zuvor lediglich einige Male Darts gespielt. Alle Probanden gaben vor dem Experiment eine schriftliche Einverständniserklärung ab. Die Studie wurde von der Ethikkommission der Hochschule für Medizin in Osaka zugelassen, und alle Verfahren stimmten mit der Deklaration von Helsinki überein.
Aufgabe und Geräte
Jede Testperson absolvierte seine Würfe auf eine E-Dart Scheibe, die den allgemeinen Regeln entsprach. Die Mitte des Bullseye befand sich in einer Höhe von 173 cm über dem Boden, die horizontale Entfernung von der Abwurflinie zur Vorderseite des Dartboards entsprach 244 cm. Die Probanden durften ihre Körperhaltung beim Wurf frei wählen und sollten stets auf die Mitte des Bullseye zielen, welches einen Durchmesser von 4,4 cm besaß. Nach 10 bis 20 Probewürfen sollte jede Testperson 20 Durchgänge absolvieren, jeder Durchgang bestand aus drei Würfen, macht 60 Würfe insgesamt. Die Probanden durften sich einen von drei zur Verfügung stehenden Darts aussuchen. Die Variationen waren dabei: lang, Länge 14,8 cm, Gewicht 18,5 Gramm, medium, Länge 14,0 cm, Gewicht 18,2 Gramm oder kurz, Länge 13,2 cm, Gewicht 18,0 Gramm. Um die Bewegung der Darts verfolgen zu können, wurde hinter dem Flight eine Markierung in Form einer Kugel (Radius 3,5 mm) angebracht. Außerdem wurde vorne am Schaft ein reflektierendes Klebeband angebracht (siehe Abbildung 1). Obwohl die zur Verfügung stehenden Darts etwas von den überlicherweise durch die erfahrenen Spieler verwendeten abwichen, konnten sich die Experten durch einige Übungswürfe daran gewöhnen. Die gleichen Markierungen in Form einer Kugel (Radius 3,5 mm) wurden auch am Zeigefinger der Testpersonen angebracht und an den Verbindungen der Fingergelenke (MP), Handgelenk, Ellbogen und der Schulter des Wurfarmes (Radius 10 mm). Die Bewegungen der Markierungen wurden mit sieben 480-Hz Infrarot-Kameras (Oqus300 von Qualisys) aufgenommen. Die mittlere Standard-Abweichung (SD) wurde auf 0.45 ± 0.05 mm kalibriert.

Abbildung 1. Darts mit zwei Markierungen.
Von links nach rechts sind kurze, mittlere und lange Darts zu sehen. Jeder Proband wählte die bevorzugte Größe aus.
Um den tatsächlichen Treffpunkt im Dartboard zur ermitteln, wurde während des Experimentes eine 30-Hz Videokamera (GZ-MG40 von Victor) hinter den Testpersonen positioniert. Die Position des Treffers wurde durch eine zweidimensionale Abbildung manuell digitalisiert und berechnet. Die mittlere Standardabweichung betrug 0,88 ± 0,19 mm. Diese Daten wurden lediglich genutzt, um sie mit der berechneten Position zu vergleichen (siehe "Zeitreihenberechnung der vertikalen Fehler").
Datenverarbeitung
Die aufgenommenen Daten wurden durch eine Spektralanalyse Technik gefiltert [18], wobei das Zeitfenster ein Viertel der Daten betrug und zwei von sechs Hauptkomponenten genutzt wurden. Nach der Datenglättung, interpolierten wir die Daten mit einer kubischen Spline-Funktion bei 1000 Hz, um die Schwankungen beim Timing mit einer Genauigkeit von 1 ms bestimmen zu können. Die Bewegung des Dart Schwerpunktes (CG) wurde durch die Bewegungen der beiden Markierungen auf dem Dart berechnet, und die relative Position des Dart Schwerpunktes unmittelbar vorher gemessen. Der Abwurf Zeitpunkt wurde für den Moment definiert, bei dem die Geschwindigkeit des Dart Schwerpunktes relativ zum Zeigefinger eine vordefinierten Punkt überschritt. Da die relative Geschwindigkeit für einige Testpersonen vor dem Abwurf schwankte, wurden unterschiedliche Punkte definiert (0,22 bis 0,46 m/s). Die Datenverarbeitung führten wir mit MATLAB von Math Works durch.
Zeitreihenberechnung der vertikalen Fehler
Wir mussten für jeden Punkt der Bewegungskurve der Hand die Fehler in der vertikalen Ebene berechnen. Für die Berechnung nutzten wir die Bewegung des Zeigefingers. Die Nutzung des Zeigefingers erlaubte uns, die Fehler in der vertikalen Ebene als Zeitreihenfehler abzuschätzen, einschließlich der Zeit hinter dem jeweiligen Abwurf (Abbildung 2). Wir gingen davon aus, dass sich der Dart genau mit dem Zeigefinger bewegt, und dass er nach dem Abwurf der parabolischen Kurve eines Massepunktes folgt, den Luftwiderstand und die Rotation vernachlässigend. Die Gleichung für den vertikalen Fehler (Ey) auf dem Dartboard wurde für den Zeitpunkt t wie folgt beschrieben:
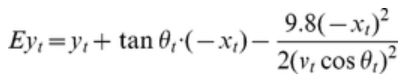
Wobei xt und yt die Positionen relativ zum Mittelpunkt des Bullseye sind, vt ist die Geschwindigkeit und θt ist die Bewegungsrichtung des Zeigefingers in der vertikalen Ebene zur Zeit t. Diese Berechnung basiert auf den Analysen der Studie von Smeets et al. [4] sowie Cohen und Sternad [9].
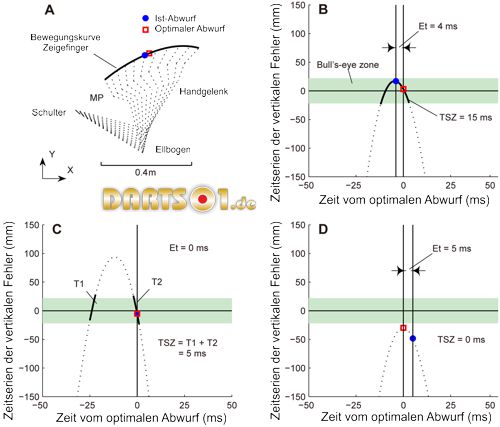
Abbildung 2. Beispiel einer Zeitreihe der vertikalen Fehlerkurven und Definitionen der relevanten Variablen.
A: Gezeigt wird eine Seitenansicht der Bewegung des Zeigefingers, 50 ms vor und nach dem eigentlichen Abwurf. Die gestrichelte Linie zeigt den Wurfarm in 10 ms Intervallen in Form eines Strichmännchens. Die Koordinatendaten des Fingergelenkes (MP), Handgelenkes, Ellenbogen und der Schulter wurden nur verwendet, um die Strichmännchen zeichnen zu können. B-D: Eine gekrümmte Linie stellt die Zeitreihe der vertikalen Fehler dar, die von der Bewegung des Zeigefingers berechnet wurde (Position, Geschwindigkeit und Richtung der Bewegung). Die durchgezogene horizontale Linie zeigt an, wo der vertikale Fehler gleich Null ist. Der horizontale grüne Schatten zeigt den Erfolgsbereich für das benötigte Ziel an. Timing Fehler (Et) wurden als absolute Differenz zwischen dem tatsächlichen und dem optimalen Abwurf definiert. Die Zeit im Erfolgsbereich (TSZ) wurde als die Zeitmenge definiert, in der die Kurve im Erfolgsbereich lag, sie wird mit fetten schwarzen Linien dargestellt. Wenn die Kurve den Erfolgsbereich zweimal kreuzt, wird TSZ (Zeit im Erfolgsbereich) als die Summe der beiden Werte (C) quantifiziert. Wenn die Kurve nicht in den Erfolgsbereich eintritt, ist TSZ gleich Null. Wir nannten diese Bahn eine "Nicht getroffen Flugbahn" (D).
Weil einige Würfe eine inakzeptable Differenz zwischen Eyt und den manuell digitalisierten Daten bezogen auf die Fehler aufwiesen (> 4 cm), wurden diese von der Analyse ausgeschlossen. Der Mittelwert ± SD der Anzahl ausgeschlossener Versuche betrug für jeden Probanten 3,6 ± 3,4. Die berechneten Trefferpunkte stimmten gut mit den digitalisierten Trefferpunkte überein (Der Korrelationskoeffizient betrug 0,86 ± 0,14). Die Standardabweichung der Differenz zwischen den berechneten und den digitalisierten Trefferpunkten betrug 18,5 ± 2,8 mm.
Abhängige Variablen
In Abbildung 2A sehen wir ein Beispiel für die Bewegungsbahn des Zeigefingers anhand des Wurfarmes eines Strichmännchens. Abbildung 2B zeigt die Zeitreihen der vertikalen Fehler, die von der Bewegungsbahn des Zeigefingers berechnet wurden. Weitere typische Beispiele für die Zeitreihenhöhenfehler zeigen die Abbildungen 2C und 2D. Basierend auf die Zeitreihenhöhenfehler berechneten wir die folgenden Variablen, bezogen auf die Schwankungsbreite beim Abwurf und die Bewegungsmuster der Hand.
Leistungsergebnis
Wir rechneten mit zwei Variablen, dem Leistungsfehler und der Erfolgsquote, um die Wurfgenauigkeit in der vertikalen Ebene zu bewerten. Weil wir uns auf die vertikale Ebene fokussierten, wurde in unserer Studie ein erfolgreicher Versuch für den Fall definiert, dass der Dart in Höhe des Bullseye landete, unabhängig vom horizontalen Ergebnis. Daher wurde der Leistungsfehler als Absolutwert des vertikalen Fehlers, Ey, zum tatsächlichen Zeitpunkt des Abwurfes definiert, Gleichung (1). Die Erfolgsquote wurde als Verhältnis der Anzahl der Würfe mit Leistungsfehlern kleiner als 22 mm zu der Gesamtzahl der Würfe jedes Probanden definiert. Grundsätzlich kann die Spielstärke beim Darts nach der Anzahl der Treffer in nächster Nähe des Ziels, einschließlich der horizontalen Ebene beurteilt werden. Unsere beiden vertikalen Variablen, Leistungsfehler und Erfolgsquote, standen in starker Wechselbeziehung mit der Trefferquote des Bullseye (Leistungsfehler: r= -0.90, Erfolgsquote: r = 0.95). Daher sind unsere beiden Variablen vernünftige Kennzahlen, um die Leistungen der Gruppen zu vergleichen.
Genauigkeit des Timings
Wir berechneten die Timing Fehler (Et), um die Genauigkeit des Abwurfzeitpunktes zu bewerten. Mehrere frühere Studien untersuchten die Präzision beim Abwurf Timing. In diesen Studien wurde das Abwurf Timing mit einem kinematischen Orientierungspunkt synchronisiert (beispielsweise, wenn sich die Hand vertikal im Raum befand [10],[19]). Dann wurde die Veränderlichkeit des Timings durch Standardabweichung berechnet. Smeets et al. [4] stellten fest, dass dieses Verfahren nicht ausreicht, um die Timing-Genauigkeit zu beschreiben, da der kinematische Orientierungspunkt als Referenz genutzt, ebenfalls variabel war. Cohen und Sternad [9] verwendeten eine andere Methode, um die Timing-Genauigkeit zu quantifizieren. Sie bestimmten die "Zeitfehler" als die absolute Differenz zwischen den tatsächlichen und den optimalen Abwürfen, den Abwurf als Folge des minimalen Fehlers während des entsprechenden Wurfes. Mit dieser Methode kann man beurteilen, ob Dartspieler den Dart innerhalb der Bewegungskurve der Hand bei jedem Wurf zum optimalen Zeitpunkt loslassen. In der vorliegenden Studie wurden die Timing-Fehler auf der Grundlage der Analyse von Cohen's Studie berechnet. Wenn die Zeitreihenfehler zweimal die "0" Zeile überschritten, wurde der Moment, der zeitlich näher zum eigentlichen Abwurf war, als optimaler Abwurf gewählt (Abbildung 2). Dann wurde Et (Timing Fehler) als die absolute Differenz zwischen dem optimalen und dem tatsächlichen Abwurf berechnet. Der Wert wurde über alle Würfe jedes Probanden gemittelt.
Weil Et kein Maß für die Streuung ist, ist es schwierig, die Präzision des Timings mit derjenigen der früheren Studien zu vergleichen. Also haben wir zusätzlich die Veränderlichkeit des Timings als Standardabweichung des Abwurf Timings in Hinsicht auf den Scheitelpunkt der Handbewegung berechnet, um unsere Ergebnisse mit denen anderer Studien vergleichen zu können.
Zeit im Erfolgsbereich
Wir wollten klären, ob ein Werfer bestimmte Muster der Handbewegung hatte, die die Schwankungen des Timings kompensieren konnten. Um dies zu erreichen, quantifizierten wir die Zeit im Erfolgsbereich (TSZ) als die Dauer, für die die Kurve der Zeitserie der vertikalen Fehler in dem Bereich lag, der zum Erfolg führte (der Erfolgsbereich). Die Zeitreihenkurve der vertikalen Fehler stellt die Bewegungsmuster der Hand dar, wobei eine längere TSZ (Zeit im Erfolgsbereich) für ein besonderes Bewegungsmuster der Hand steht, mit einem längeren Zeitfenster, das zum Erfolg führen kann. Wenn die Kurve den Erfolgsbereich zweimal kreuzt, wird TSZ (Zeit im Erfolgsbereich) als die Summe der beiden Werte berechnet (Abbildung 2C). Wenn die Kurve nicht in den Erfolgsbereich eindringt, ist TSZ gleich Null. Wir nannten diese Bahn eine "Nicht getroffen Flugbahn" (Abbildung 2D).
Die TSZ (Zeit im Erfolgsbereich) wurde über erfolgreiche Würfe gemittelt, für jeden Probanden. Sobald Fehlwürfe, die aus "Nicht getroffen Flugbahnen" resultierten, in der Variable enthalten waren, wäre die durchschnittliche TSZ verzerrt, weil in diesen Fällen ein Wert von Null zugeordnet wurde. Deshalb zeigt ein Durchschnitt aller Würfe eines jeden Probanten nicht wirklich die normalen Muster der Bewegungskurve der Hand. Die Anzahl der erfolgreichen Würfe der erfahrenen Spieler reichte von 25 bis 57, während die Treffer der Anfänger bei 8 bis 24 lagen.
Schwankungsbreite als Kurve der Zeitreihenfehler in der vertikalen Ebene
Die Kurven der Zeitreihenfehler in der vertikalen Ebene entsprechen den Bewegungsmustern der Hand, einschließlich der Position, Geschwindigkeit und Bewegungsrichtung. Deshalb stellt die Schwankungsbreite der Kurven für jeden Probanden die Schwankungsbreite der Bewegungsmuster der Hand dar. Um dies zu bewerten, berechneten wir die Standardabweichungen der Spitzen der Zeitreihenfehlerkurven, weil diese in geeigneter Weise die Eigenschaften dieser Kurven anzeigen (Abbildungen 2B-D). Wir berechneten die Standardabweichungen der Spitzenwerte und Spitzenzeiten, die mit dem Zeitpunkt des optimalen Abwurfes für jeden Probanden synchronisiert wurden.
Statistiken
Wir nutzten Wilcoxon-Rangsummentests, um die Unterschiede zwischen sechs Variablen zu bewerten, zwischen der Gruppe der erfahrenen Spieler und der Anfängergruppe. Die statistische Signifikanz wurde mit p<0,05 festgelegt.
Ergebnisse
Leistungs Ergebnisse
Der Mittelwert der Leistungsfehler war für die Expertengruppe deutlich kleiner als für die Anfängergruppe (Abbildung 3A: W = 36, p<0,05). Der Mittelwert der Erfolgsrate war für die Expertengruppe signifikant höher als für die Anfängergruppe (Abbildung 3B: W = 100, p<0,05). Der stärkste Spieler aller Probanten in Bezug auf die Leistungsfehler war Experte 1 (Leistungsfehler = 13,5 mm, Erfolgsquote = 77,0%), und Experte 2 relativ zur Erfolgsrate (Leistungsfehler = 14,4 mm, Erfolgsquote = 79,2%). Diese Spieler werden in einem späteren Abschnitt als erfolgreiche Beispiele verwendet werden. Der schlechteste Spieler aus der Gruppe der Experten war nach beiden Messmethoden besser als der beste Spieler aus der Gruppe der Anfänger. Dies bestätigt, dass langfristiges Training die Genauigkeit des Wurfes verbessert.
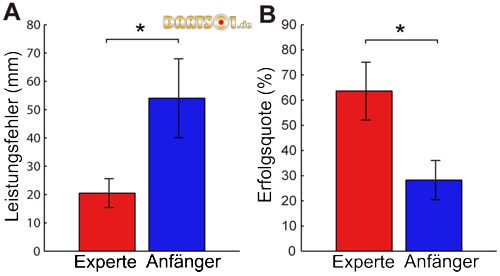
Abbildung 3. Mittlere Leistungsfehler und Erfolgsquote.
Die Leistungsfehler (A) und Erfolgsquote (B) wurden pro Gruppe gemittelt und durch Balken angezeigt. Die Fehlerbalken bezeichnen die Standardabweichungen zwischen den Probanden. *: p<0,05.
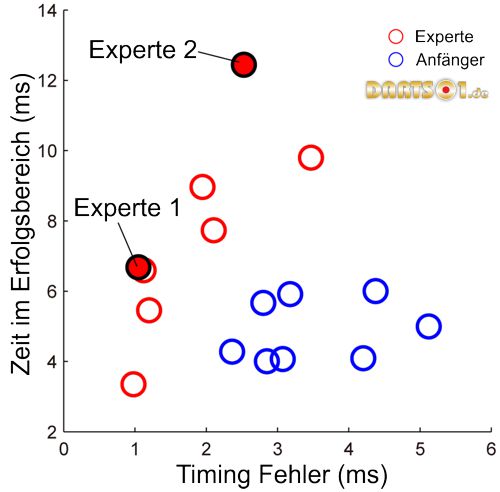
Typische Muster der Zeitreihenfehler in der vertikalen Ebene
Wir fanden zwei typische Strategiearten in der Expertengruppe, und einen anderen Typ in den Gruppe der Anfänger. Drei typische beispielhafte Kurven der Zeitreihenfehler in der vertikalen Ebene für alle Würfe eines jeden Probanten zeigen wir in Abbildung 4. In der vorliegenden Studie haben wir unter Verwendung der Bewegung des Zeigefingers die Fehler in der vertikalen Ebene als Zeitreihe berechnet. Somit stellen die Kurven dieser Zeitreihenfehler die Muster der Bewegungskurve der Hand dar, einschließlich der Position, der Geschwindigkeit und Bewegungsrichtung. Eines der typischen Muster, dargestellt in der linken Spalte der Abbildung 4, zeigt relativ konstante Würfe und überlappt für eine beträchtliche Zeit den Erfolgsbereich (d.h. die Muster dieser Probanden zeigen, dass sie längere TSZs hatten). Dies bedeutet, dass diese Probanden ein längeres Zeitfenster für den Abwurf hatten, um ein genaues Ergebnis erzielen zu können. Aber der Wertebereich für Et (Timing Fehler) war für diese Probanden ähnlich dem Wertebereich der Anfänger. Das heißt, dass sie Bewegungsmuster der Hand hatten, die die Timing-Fehler beim Abwurf kompensieren konnten. Der zweite Satz beispielhafter Kurven, dargestellt in der mittleren Spalte von Abbildung 4, zeigt hohe Konstanz. Die Dauer der TSZ (Zeit im Erfolgsbereich) war für diese Probanden ähnlich der TSZ der Anfänger, aber ihr Timing beim Abwurf lag gebündelt in der Nähe des optimalen Abwurfzeitpunktes. Somit war Et (Timing Fehler) gering. Diese Probanden hatten keine ergänzenden Bewegungsmuster der Hand gewählt, aber die Fehler beim Timing extrem reduziert, was zu genauen Ergebnissen führte. Der dritte Kurventyp, dargestellt in der rechten Spalte der Abbildung 4, zeigt eine größere Schwankungsbreite, geringere TSZ Werte und einen größeren Wertebereich für Et. Dieses Muster wurde nur von Teilnehmer aus der Anfängergruppe gezeigt. Anfänger konnten keine dauerhaft genauen Ergebnisse erzielen, da sie weder über ergänzende Bewegungsmuster der Hand noch geringe Fehler beim Abwurftiming verfügten.
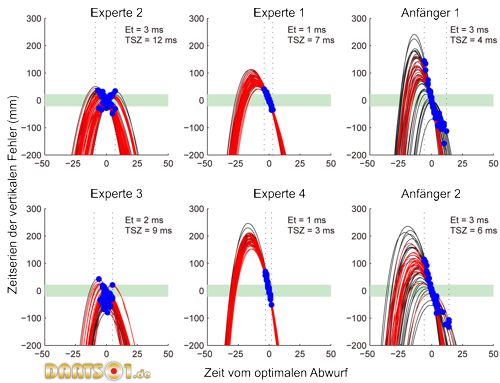
Abbildung 4. Beispiele für Zeitreihenfehler in der vertikalen Ebene
Die Zeitreihen Fehlerkurven von vier Experten und zwei Anfängern. Die Zeit wurde mit dem optimalen Abwurf synchronisiert. Rote Linie: erfolgreicher Wurf. Blaue Punkte: tatsächlicher Moment des Abwurfes. Grün unterlegt: Erfolgsbereich. Vertikal gepunktete Linien: Bereich von Et (Timing Fehler).
Vergleiche zwischen den Gruppen der Experten und Anfänger
Der Mittelwert der Timingfehler (Et) war für die Gruppe der Experten deutlich kleiner als für die Anfängergruppe (Abbildung 5A: W = 42, p<0,05). Das heißt, dass die erfahrenen Spieler ihre Darts näher an dem Punkt abwarfen, der zu minimalen Fehlern bei jedem Wurf führte. Jedoch zeigten einige Experten Würfe mit Werten des Et, ähnlich denen der Anfänger-Gruppe (Experten 2 und 3 in Abbildung 4), und einige Experten zeigten extrem kleine Werte von Et, in der Größenordnung von 1 ms. Experte 4 hatte mit 0,98 ± 1,13 ms (Abbildung 4) den geringsten Wert, und vier der acht erfahrenen Dartspieler zeigten Werte des Et kleiner als 1,2 ms (Abbildung 6).
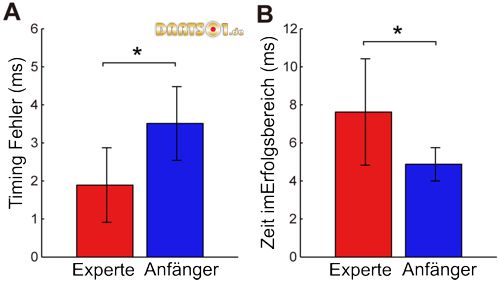
Abbildung 5. Mittlere Timingfehler und Zeit im Erfolgsbereich.
Der Timingfehler (A) und die Zeit im Erfolgsbereich (B) wurden pro Gruppe gemittelt und mit Balken dargestellt. Die Fehlerbalken kennzeichnen die Standardabweichungen zwischen den Probanden. *: p <0,05.
Die Experten, die kleine Werte für Et (Timing Fehler) zeigten, hatten relativ kurze TSZs (Zeiten im Erfolgsbereich) (Abbildung 6). Ihre TSZs wichen nicht von denen aus der Anfängergruppe ab. Andererseits zeigten die Experten die gleichen Et wie die Anfängergruppe, mit höheren TSZ-Werten. Der Mittelwert der TSZ war für die Expertengruppe signifikant höher als für die Anfängergruppe (Abbildung 5B: W = 89, p<0,05), obwohl die Hälfte der Experten ähnliche Werte wie die Anfängergruppe zeigten. Dies passierte, weil die andere Hälfte der Experten große TSZs hatten. Experte 2 hatte unter allen Probanden den höchsten TSZ-Wert (12,4 ms). Das bedeutet, dass Experte 2 ein Zeitfenster von 12,4 ms für den Abwurf hatte, um das Ziel genau zu treffen.
Somit fanden wir zwei Strategiearten in der Gruppe der Experten. Jeder der beiden Experten mit den besten Leistungen (die Experten 1 und 2) wählte eine dieser Strategien.
Der Mittelwert der Variabilität bei den Spitzen der Zeitreihenfehlerkurven war für die Gruppe der Experten deutlich kleiner als für die Gruppe der Anfänger (Experten: 21,3 ± 4,3 mm, Anfänger: 65,0 ± 13,0 mm; W = 36, p<0,05). Der Mittelwert der Variabilität in den Zeitspitzen im Hinblick auf den optimalen Abwurfzeitpunkt war für die Gruppe der Experten ebenfalls deutlich kleiner als für die Gruppe der Anfänger (Experten: 2,1 ± 1,2 ms, Anfänger: 4,2 ± 0,7 mm; W = 39, p<0,05). Dann waren die Bewegungsmuster der Hand bei den Experten stabiler als bei den Anfängern, sowohl räumlich als auch zeitlich.
Leistungsfehler und Beziehung zwischen Et und TSZ
Um zu bestätigen, dass größere TSZs tatsächlich die Et (Timing Fehler) kompensieren können, stellten wir die Beziehung zwischen Et und den Leistungsfehlern für alle Würfe der Experten grafisch dar, mit der Unterscheidung zwischen der längsten TSZ und der kürzesten TSZ (Abbildung 7). Rote Punkte zeigen die Top-100-Würfe in der TSZ (Mittelwert ± Standardabweichung: 13,3 ± 2,2 ms), und blaue Punkte zeigen die schlechtesten 100 Würfe in der TSZ (2,7 ± 1,6 ms). Die Anzahl der insgesamt erfolgreichen Würfe für die Top-100-Würfe in der TSZ (76 Würfe) war signifikant höher als die für die schlechtesten 100 Würfe in der TSZ (44 Würfe) [Verhältnis Test mit zwei Stichproben, x 2 = 21,3; p<0,05]. Somit hatten die Würfe mit den höchsten TSZ Werten die geringste Empfindlichkeit gegenüber Et. Andererseits erhöhten sich Leistungsfehler der Würfe mit den kürzesten Zeiten im Erfolgsbereich (TSZ) dramatisch, während die Timing Fehler (Et) zunahmen.
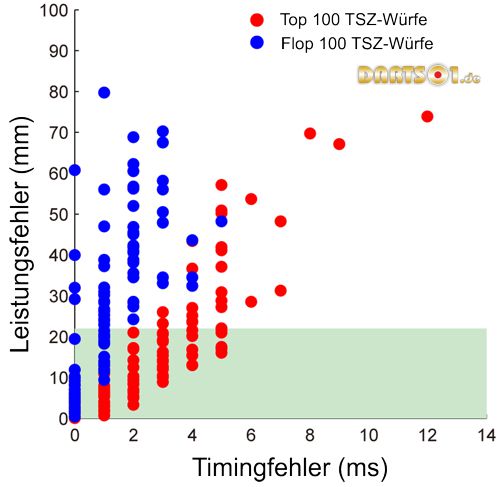
Abbildung 7. Anfälligkeit der Timingfehler für Leistungsfehler: Differenz zwischen Zeitspannen im Erfolgsbereich.
Beziehung zwischen Timingfehler und Leistungsfehler aller Würfe der Experten. Die roten Punkte zeigen die Top-100-Würfe, die längere TSZs haben, und die blauen Punkte zeigen die schlechtesten 100 Würfe.
Beziehung zwischen Et und Timing-Variabilität
Eine andere Annahme für die Präsision des Timings war die Variabilität des Timings. Die Mittelwerte waren zwischen den Experten und Anfängern statistisch gesehen nicht unterschiedlich (Experten: 2,4 ± 1,2 ms, Anfänger: 2,4 ± 0,6, W = 62, p = 0,57). Es gab eine starke Korrelation zwischen Et und der Variabilität des Timings bei den Experten (r = 0,93), bei den Anfängern gab es hingegen keine Korrelation (r = 0,19) (Abbildung 8). Es konnte gezeigt werden, dass einige Anfänger trotz großer Et kleine Variabilitäten beim Timing bewiesen.
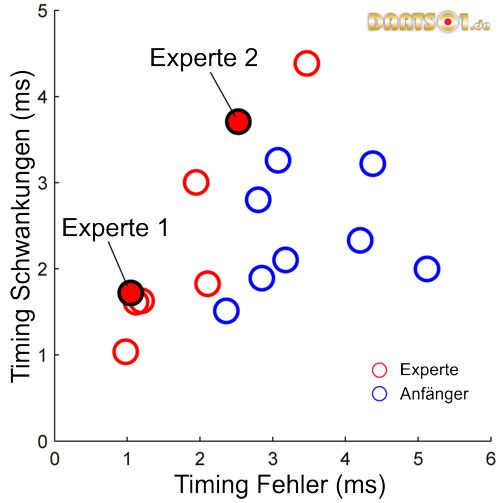
Abbildung 8. Beziehung zwischen Timingfehlern und Variabilität des Timings.
Jeder Kreis zeigt die Daten für einen Probanden. Die absolute Differenz zwischen den tatsächlichen und den optimalen Abwürfen war der Timingfehler. Die Variabilität beim Timing war die Standardabweichung des tatsächlichen Abwurfes, in Bezug auf den Höhepunkt der Bewegungskurve der Hand.
Diskussion
Das Ziel der vorliegenden Studie war es zu untersuchen, ob erfahrene Dartspieler Muster beim Bewegungsablauf der Hand haben, die zwangsläufig auftretende Schwankungen beim Abwurf-Timing kompensieren können. Wir verglichen die Timing-Genauigkeit und Bewegungsmuster der Hand zwischen erfahrenen Spielern und Anfängern. Die Ergebnisse zeigten, dass die Expertengruppe weniger Fehler in ihrem Abwurf-Timing hatte und weitere ergänzende Handbewegungsmuster als die Anfängergruppe aufwies. Diese Ergebnisse unterstützten unsere Hypothese. Allerdings fanden wir in der Expertengruppe zwei typische Wurfstrategien. Insbesondere wählten die beiden besten Werfer (Experten 1 und 2) deutlich unterschiedliche Strategien. Die Eigenschaften dieser Strategien werden nachstehend diskutiert.
Strategie der ergänzenden Bewegungsmuster der Hand
Eine Strategie bezog Bewegungsmuster der Hand mit ein, die Schwankungen beim Timing kompensieren konnte, um konstant präzise Würfe abzuliefern. Experte 2 nutzte diese Strategie. Auch wenn seine Timing-Fehler sich nicht von den Fehlern der Anfänger unterschieden, kompensierte er die Timing-Fehler durch eine modifizierte Handbewegung. Dieses Ergebnis deckt sich mit den Ergebnissen der Studie von Cohen und Sternad [9], die zeigten, dass erfahrende Probanden ihren Bewegungsablauf optimierten, um Schwächen bei den Timing-Schwankungen auszugleichen. Sie erwähnten, dass ein wesentlicher Vorteil dieser Strategie darin liegt, dass der Bewegungsablauf im Voraus geplant werden kann, und der Werfer sich nicht auf das Feedback des aktuellen Wurfes verlassen muss. Die Bewegungen beim Dartwurf sind zu schnell, um Korrekturen, basierend auf propriozeptiver Information vorzunehmen [20]-[22]. Es kann spekuliert werden, dass die Probanden, die diese Strategie nutzten, die Bewegungsabläufe ihrer Hand vorplanten, welche die Empfindlichkeit bei den Schwankungen des Abwurf Timings reduzieren könnten.
Strategie zur Verringerung der Schwankungsbreite beim Abwurf Timing
Eine andere Strategie bezog eine verminderte Schwankungsbreite des Timings ein, um die Wurfgenauigkeit zu verbessern. Vier erfahrende Spieler, einschließlich Experte Nr. 1, zeigten diese Strategie und reduzierten ihre Timing-Fehler auf den niedrigen Wert von 1 ms. Diese Strategie wurde anstelle eines ergänzenden Bewegungsmusters der Hand genutzt, um einen genauen Wurf zu erzielen.
Calvin [5] sowie Chowdhary und Challis [6] berichteten, dass das Zeitfenster des Abwurfes theoretisch kürzer als 1 ms sein muss, um eine hohe Genauigkeit zu erreichen. Hore und Watt [23] zeigten, dass Hochschulbaseballspielern eine Reihe von aufeinanderfolgenden Würfen mit Abwurf Timings von nur 1 ms gelangen. Die Ergebnisse unserer vier Experten, die die Strategie der Verringerung von Et zeigten, scheinen die Ergebnisse dieser früheren Studien zu unterstützen [5],[6],[23]. Aufgrund von Unterschieden in den Definitionen der Genauigkeit beim Timing, können unsere Ergebnisse der Timing-Fehler jedoch nicht einfach mit den früheren Studien verglichen werden, welche die Schwankungsbreite beim Timing als Standardabweichungen in Bezug auf einen kinematischen Orientierungspunkt abschätzten. Deshalb berechneten wir auch die Schwankungsbreite beim Timing synchronisiert mit dem Höhepunkt der Handbewegung. Die Schwankungsbreite beim Timing lag für unsere vier Experten zwischen 1,0 bis 1,7 ms. Diese Schwankungsbreite beim Timing des Dartwurfes war geringer als bei den Ergebnissen der Studie von Smeets et al. (3,4 bis 7,7 ms), und ihre Definition der Schwankungsbreite beim Timing war die gleiche wie unsere [4]. Sie war jedoch etwas größer als bei den Ergebnissen der Untersuchung von Hore und Watts (Durchschnitt 0,84 ms). Dieser Wert wurde aus ihrem Ergebnis abgeleitet, mit einem Zeitfenster bei 95% der Würfe (SD×3.92) für den Abwurf eines Balles in Bezug auf die vertikale Position der Hand. Hore und Watts erwähnten, dass eine präzise Kontrolle des Timings durch einen Mechanismus kam, dem Reaktionskräfte zugrunde liegen. Die erfahrenen Werfer erreichten in ihrer Studie eine Kontrolle des Timings mit einer Schwankungsbreite von 1 ms, indem sie die Fingerkraft / Steifigkeit berechneten, die auf einer Schätzung der Vorschubkraft des Balles beruhten, die durch die Handbewegung erzeugt wurde. Da sich Darts vom Ballwurf in Bezug auf das Gewicht des Geschosses, der Beschleunigung des Armes und der Richtung der Finger während der Beschleunigung des Armes sowie den Moment des Abwurfes unterscheidet, ist die spürbare Vorschubkraft an der Fingerspitze viel kleiner. Allerdings handelt es sich wahrscheinlich um den gleichen Mechanismus. Cohen und Sternad berichteten, dass bei der virtuellen Wurf Aufgabe, die Fehler beim Timing nach 9 ms nicht weiter anstiegen [9], was erheblich länger war, als unser Ergebnis für Et. Der große Fehler beim Timing in der Studie von Cohen und Sternad mag daraus resulierten, dass sie keinen "Vorschub Mechanismus" einbezogen. Bei ihrer Aufgabe wurde der Abwurf basierend auf der Streckung des Zeigefingers bestimmt.
Messung der Präsision des Timings
Die Werte von Et waren zwischen den Experten und der Anfängergruppe signifikant unterschiedlich, aber die Werte der Schwankungsbreite des Timings unterschieden sich nicht. Das lag daran, dass die Experten mit größere Et Werten auch höhere Werte bei den Schwankungen des Timings aufwiesen, aber einige Anfänger trotz höherer Et Werte geringere Schwankungen beim Timing aufwiesen (Abbildung 8). Das heißt, dass diese Anfänger eine ziemlich gute räumliche Kontrolle des Abwurfes, synchronisiert mit dem Höhepunkt ihrer Handbewegung zeigten. Allerdings waren ihre Bewegungsmuster der Hand, einschließlich der Geschwindigkeit und der Bewegungsrichtung, sehr unbeständig. Wenn die Schwankungen der Bewegungsmuster der Hand den Zeitpunkt des optimalen Abwurfes beeinflussen, treten Timing Fehler (Et) auf. Die erfahrenen Spieler, die die Schwankungsbreite beim Timing reduzierten, zeigten sehr wenig Schwankungen sowohl bei den Timing Fehlern (Et) als auch bei den Timing Schwankungen (Experte 1 hatte z.B. ein Et von 1.0 ms und eine Timing Schwankung von 1.7 ms). So bewegten die erfahrenen Spieler ihre Hände stereotyp und zeigten eine engere Verknüpfung zwischen Timing und Handbewegung. Andererseits zeigten die erfahrenen Spieler, die ergänzende Handbewegungsmuster nutzten, größere Schwankungen, sowohl bei den Timing Fehlern (Et) als auch bei der Timing Schwankung (Experte 2 hatte z.B. einen Et von 2,6 ms und eine Timing Schwankung von 3,7 ms). Diese erfahrenen Spieler reduzierten ihre Empfindlichkeit gegenüber den Timing Schwankungen. Auf diese Weise wurde der Wert der Timing Präzision durch den genutzten Orientierungspunkt (dem optimalen Einfluss oder höchsten Punkt der Bewegungskurve der Hand) beeinflusst. Es ist unmöglich zu sagen, welche Maßnahme besser ist, da dies vom Zweck der Forschung abhängt.
Welche Strategie ist vorteilhafter?
Warum wählten einige der erfahrenen Spieler nicht die Strategie, die die Schwankung des Timings kompensieren könnte? Eine mögliche Erklärung ist, dass diese Probanden ein gewisses Risiko vermieden. Um eine längere TSZ zu erreichen, ist es notwendig, die Spitzen der Zeitserien der vertikalen Fehlerkurve im Erfolgsbereich zu platzieren. Es scheint jedoch, dass die Verwendung solcher Bewegungsmuster der Hand, die Möglichkeit einer "Nicht getroffen Flugbahn" (Abbildung 2D) verglichen mit einem Muster, bei dem die Spitze oberhalb des Erfolgsbereiches liegt (z.B. die Experten 1 und 4 in Abbildung 4) erhöht. In der Tat generierte Experte 3, dessen TSZ bei 9,0 ms lag (Abbildung 4) "Nicht getroffen Flugbahnen" in 33% all seiner Würfe, und seine Leistung war die niedrigste in der Gruppe der erfahrenen Spieler (Leistungsfehler = 25,2 mm, Erfolgsquote = 53,5 %). Somit kann ein solches Muster die Schwankungsbreite beim Timing kompensieren, hat aber ein zwangsläufiges Risiko zur Folge, "Nicht getroffen Flugbahnen" zu produzieren. Sternad et al. [24] berichteten auch, dass bei einer virtuellen Wurf Aufgabe, einige Probanden Strategien mit hohem Fehlerpotenzial wählten, während andere riskante Strategien vermieden. Es wird angenommen, dass die individuellen Unterschiede bei der Auswahl der Strategien, die Gefahr beinhalten, die Vorlieben des Einzelnen widergespiegelt werden [25]-[27]. In der aktuellen Studie mag die gewählte Strategie eines Dartspielers seine individuelle Einstellung gegenüber dem Risiko eine "Nicht getroffen Flugbahn" zu produzieren, reflektiert worden sein.
Die Kurven der Zeitreihen-Fehler der Anfänger waren unbeständiger als die aus der Expertengruppe. Diese Unbeständigkeit zeigt jedoch nicht einfach die "Störungen" der Schwankungen von Versuch zu Versuch. Die Schwankungen in der Frühphase motorischen Lernens zeigt die Auseinandersetzung mit der Aufgabe und hilft bei der Suche nach den besten Lösungen, um das gewünschte Ergebnis zu erzielen [28]. Fast alle erfolgreichen Würfe der Anfänger bezogen Muster ein, die das Risiko vermieden, eine "Nicht getroffen Flugbahn" zu produzieren (Rote Linie der Anfänger in Abbildung 4). Dennoch hatten einige Würfe eine längere TSZ und produzierten erfolgreiche Treffer (Anfänger 2 in Abbildung 4). Wenn dieses Muster wiederholt die Timing-Fehler kompensierte und zum Erfolg führte, würde der Dartspieler dieses vorteilhafte Muster erlernen. Durch die Sondierung nach der besten Lösung, konnten diejenigen Dartspieler, die ein ergänzendes Muster erfuhren damit beginnen, eine solche Strategie zu adoptieren. Andererseits mögen diejenigen Dartspieler, die ein solches Muster als unzureichend erlebt hatten, ihre Schwankungsbreite beim Timing reduziert haben. Alternativ mögen diejenigen Dartspieler, die ihre Schwankungsbreite beim Abwurf Timing reduzieren konnten, um ihre gewünschte Leistung zu erzielen, nicht die ergänzenden Bewegungsmuster der Hand erlernen müssen.
In der aktuellen Studie, verwendeten unsere beiden besten Dartspieler unterschiedliche Strategien. Deshalb können wir nicht feststellen, ob für konstant präzise Würfe die eine Strategie vorteilhafter ist als die andere. Darts wird in einem gleichbleibenden Umfeld gespielt und wird nicht durch die Umgebung oder andere Spieler beeinflusst. Darüber hinaus ist für Darts eine relativ einfache Bewegung erforderlich, die vor allem mittels Beugung und Streckung des Ellbogens durchgeführt wird. Diese Charakteristika können es Dartspielern ermöglichen, durch eine geringe Schwankungsbreite eine bessere Kontrolle ihres Abwurf Timings zu erlangen. Wenn eine Aufgabe eine Fertigkeit aus einer instabilen Haltung oder in einem sich veränderden Umfeld beinhaltet, wie beim Sprungwurf im Basketball oder dem Wurf eines Feldspielers beim Baseball, wäre die ergänzende Strategie besser, um genaue und präzise Würfe zu produzieren.
Grundsätzlich ist eine Reduzierung der Bewegung und Schwankung beim Timing der beste Weg, um eine Verbesserung bei Genauigkeit und Präzision des Wurfes zu erzielen. Die Ergebnisse der vorliegenden Studie zeigen, dass eine Veränderung der Bewegungsrichtung der Hand, in Form eines ergänzenden Musters ebenso effektiv sein kann, wie eine Reduzierung der Schwankungsbreite. Lernende und Trainer, die dieses Konzept verstehen, könnten dieses Wissen nutzen, um die Genauigkeit zu verbessern. Ferner sei auch darauf hingewiesen, dass die bessere Strategie in Abhängigkeit von den Eigenschaften der Aufgabe und dem Individuum gewählt werden sollte.
Beiträge der Autoren
Konzept und Design der Experimente: Daiki Nasu, Tomoyuki Matsuo. Durchführung der Experimente: Daiki Nasu, Tomoyuki Matsuo. Datenanalyse: Daiki Nasu Niederschrift der Studie: Daiki Nasu, Tomoyuki Matsuo, Koji Kadota. Übersetzung: Jürgen Schmitz
Referenzen
- Hore J, Watts S, Tweed D (1996) Errors in the control of joint rotations associated with inaccuracies in overarm throws.
- Hore J, Watts S, Tweed D, Miller B (1996) Overarm throws with the nondominant arm: kinematics of accuracy.
- Hore J, Timmann D, Watts S (2002) Disorders in timing and force of finger opening in overarm throws made by cerebellar subjects.
- Smeets JBJ, Frens MA, Brenner E (2002) Throwing darts: timing is not the limiting factor.
- Calvin WH (1983) A stone’s throw and its launch window: timing precision and its implications for language and hominid brains.
- Chowdhary AG, Challis JH (1999) Timing accuracy in human throwing.
- Newell KM, Corcos DM (1993) Issue in variability and motor control. In: Newell KM, Corcos D, editors. Variability and motor control. Champaign: Human Kinetics.
- Faisal AA, Selen LPJ, Wolpert DM (2008) Noise in the nervous system.
- Cohen RG, Sternad D (2012) State space analysis of timing: exploiting task redundancy to reduce sensitivity to timing.
- Hore J, Watts S, Martin J, Miller B (1995) Timing of finger opening and ball release in fast and accurate overarm throws.
- Timmann D, Citron R, Watts S, Hore J, Marsden J, et al. (2001) Increased variability in finger position occurs throughout overarm throws made by cerebellar and unskilled subjects.
- Müller H, Loosch E (1999) Functional variability and an path of movement during targeted throwing.
- Fleisig G, Chu YC, Weber A, Andrews J (2009) Variability in baseball pitching biomechanics among various levels of competition.
- Yang JF, Scholz JP (2005) Learning a throwing task is associated with differential changes in the use of motor abundance.
- Cohen RG, Sternad D (2009) Variability in motor learning: relocating, channeling and reducing noise.
- Kudo K, Tsutsui S, Ishikura T, Ito T, Yamamoto Y (2000) Compensatory coordination of release parameters in a throwing task.
- McDonald PV, van Emmerik REA, Newell KM (1989) The effects of practice on limb kinematics in a throwing task.
- Alonso FJ, Del Castillo JM, Pintado P (2005) Application of singular spectrum analysis to the smoothing of raw kinematic signals.
- Jegede E, Watts S, Stitt L, Hore J (2005) Timing of ball release in overarm throws affects ball speed in unskilled but not skilled individuals.
- Cordo P, Carlton L, Bevan L, Carlton M, Kerr GK (1994) Proprioceptive coordination of movement sequences: role of velocity and position information.
- Hore J, Ritchie R, Watts S (1999) Finger opening in an overarm throw is not triggered by proprioceptive feedback from elbow extension or wrist flexion.
- Hore J, Watts S (2005) Timing finger opening in overarm throwing based on a spatial representation of hand path.
- Hore J, Watts S (2011) Skilled throwers use physics to time ball release to the nearest millisecond.
- Sternad D, Abe MO, Hu X, Müller H (2011) Neuromotor noise, error tolerance and velocity-dependent costs in skilled performance.
- Seydell A, McCann BC, Trommershäuser J, Knill DC (2008) Learning stochastic reward distributions in a speeded pointing task.
- Nagengast AJ, Braun DA, Wolpert DM (2010) Risk-sensitive optimal feedback control accounts for sensorimotor behavior under uncertainty.
- Wolpert DM, Landy MS (2012) Motor control is decision-making.
- Newell KM (1991) Motor skill acquisition.