| Psychischer Druck | Inhaltsverzeichnis der Doktorarbeit |
Untersuchungsmethodik

5.3.7 Datenanalyse
Einschränken von Freiheitsgraden
Anhand der 2D-Bewegungsdaten wird untersucht, ob erhöhte Druckbedingungen bzw. ein ausführungsbezogener Aufmerksamkeitsfokus zu einer verminderten Nutzung von Freiheitsgraden im Bewegungsvollzug führen. Dazu werden die beiden in Abschnitt 4.1 beschriebenen Möglichkeiten zur Einschränkung von Freiheitsgraden geprüft, also (1.) die Fixierung einzelner Gelenke und (2.) die lineare Kopplung der Bewegungen verschiedener Gelenke. Beide Aspekte werden anhand der Winkelverläufe in Knie-, Hüft-, Schulter-, Ellbogen- und Handgelenk untersucht.
Das Fixieren einzelner Gelenke sollte sich in geringeren Bewegungsumfängen zeigen. Dazu wurden für jeden Wurf die minimalen und maximalen Winkelstellungen für die fünf Gelenkwinkelverläufe bestimmt und jeweils die Differenz gebildet. Für jede Wurfserie wurde daraus der Mittelwert für den Bewegungsumfang der fünf Gelenke ermittelt.
Wie in Abschnitt 4.1 beschrieben, sollte sich eine stärkere Kopplung einzelner Freiheitsgrade insbesondere bei den Gelenken zeigen, die bei der Streckbewegung nacheinander eingesetzt werden. Aus diesem Grund wird im Folgenden zur Prüfung dieses Aspekts die Koordination von Knie- und Schultergelenk, sowie von Ellbogen- und Handgelenk betrachtet (vgl. auch Abbildung 7). Dazu werden für jeden Wurf bivariate Korrelationen der Winkelverläufe von Knie- und Schulter- bzw. Ellbogen- und Handgelenk bestimmt. Um eine Beeinflussung des Korrelationskoeffizienten durch unterschiedlich viele Datenpunkte zu vermeiden (vgl. Sidaway, Heise & Schoenfelder-Zohdi, 1995), wird für die einzelnen Winkelverläufe eine zeitliche Normierung mittels linearer Interpolation vorgenommen. Für die anschließende Bestimmung von Serienmittelwerten werden die Daten einer Fisher-Z-Transformation unterzogen (Bortz, 2005, S. 218f.).
Ausführungsvariabilität und aufgabendienliche Kovariation
Die 3D-Ballflugdaten werden genutzt, um mit der Ausführungsvariabilität und der aufgabendienlichen Kovariation zwei ergebnisrelevante Faktoren zu quantifizieren, bei denen aufgrund der vermuteten Beeinträchtigung der Bewegungsausführung Veränderungen zu erwarten sind. Als Maß für die Ausführungsvariabilität wird die aufgrund der Streuung der Ausführungsgrößen zu erwartende Ergebnisvariabilität (ErwEV) genutzt. Die Bestimmung der aufgabendienlichen Kovariation erfolgt mithilfe des verallgemeinerten Kovariationskoeffizienten R für nicht-lineare multiple Zusammenhänge (Müller, 2001; Müller & Sternad, 2003).
Sowohl die empirische Ergebnisvariabilität (EmpEV) als auch die kovariationsbereinigte zu erwartende Ergebnisvariabilität (ErwEV) werden anhand der für die Flugkurven ermittelten Polynomkoeffizienten a0 , a1 , a2 , b0 und b1 bestimmt, sodass eine Beeinflussung durch unterschiedliche Messfehler ausgeschlossen werden kann (vgl. Müller, 2001, S. 149).
Für die Berechnung von EmpEV und ErwEV ist ein Maß zur Bestimmung der Ergebnisvariabilität erforderlich, das die leistungsrelevanten Abweichungen vom Ziel möglichst gut erfasst. Dazu werden die Schnittpunkte der Flugkurven des Ballmittelpunktes mit der Ringebene berechnet und der bivariate variable Fehler (Hancock, Butler & Fischman, 1995) bestimmt. Allerdings werden dabei die Abweichungen in Wurfrichtung in Abhängigkeit des Eintrittswinkels der Flugkurve in die Ringebene stärker gewichtet. Die Berechnung dieses basketballspezifischen bivariaten variablen Fehlers (BVEBB) ist in Gleichung (4) dargestellt. Dabei beschreiben (xi,yi) die Koordinaten des Eintrittspunktes der i-ten Flugkurve in die Ringebene und (x,y) die des mittleren Eintrittspunktes in einer Serie von k Würfen. Weiterhin stellt αe den mittleren Eintrittswinkel der Flugkurven einer Wurfserie in die Korbebene dar.
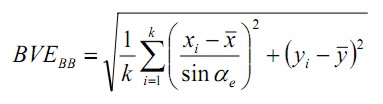 | (4) |
Für die Bestimmung des Kovariationskoeffizienten R ist es erforderlich, die kovariationsbereinigte Ergebnisvariabilität (ErwEV) zu bestimmen. Dies kann erreicht werden, indem die spezifischen Kopplungen der Ausführungsgrößen durch ein Permutationsverfahren (Müller, 2001; Müller & Sternad, 2003) aufgelöst und die Ergebnisvariabilität dann erneut bestimmt wird. Das Prinzip des Verfahrens wird im Folgenden anhand der Flugkurven von 10 Freiwürfen veranschaulicht, wobei die Betrachtungen zur Vereinfachung auf den zweidimensionalen Fall beschränkt werden. In Abbildung 14 A sind die Flugbahnen der 10 Originalwürfe dargestellt. Die zugehörigen Polynomkoeffizienten der 10 Flugkurven sind in Tabelle 2 auf der linken Seite aufgeführt. Aus den Koeffizienten werden die Schnittpunkte der Flugkurven mit der Ringebene berechnet und daraus die empirische Ergebnisvariabilität (EmpEV) ermittelt – im hier vorliegenden zweidimensionalen Fall wird dazu der variable Fehler (VE) genutzt.
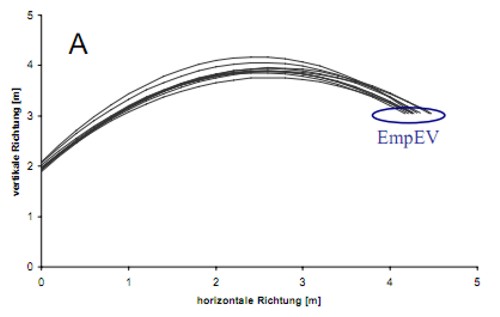
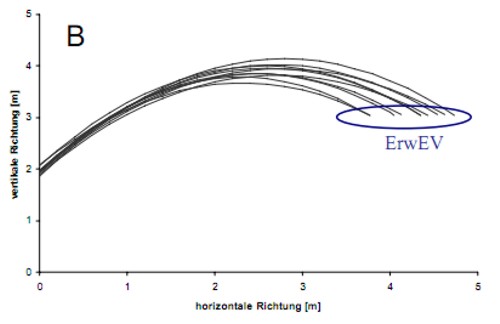
Abbildung 14 A-B: Empirisch bestimmte Flugkurven (A) und neu berechnete Flugkurven nach Aufhebung der spezifischen Kopplungen innerhalb der Würfe (B).
| Tabelle 2: Aufgeführt sind die Koeffizienten a0 , a1 und a2 der Polynome zweiter Ordnung, durch die sich die in Abbildung 14 gezeigten Flugkurven beschreiben lassen. Links sind die Koeffizienten der empirisch ermittelten Originalflugkurven dargestellt. Für die Berechnung der neuen Flugkurven werden die gleichen Koeffizienten in einer neuen Zusammensetzung genutzt. | ||||||
| Originalflugkurven | Neu berechnete Flugkurven | |||||
| a2 | a1 | a0 | a2 | a1 | a0 | |
| Wurf 1 | -0,303 | 1,534 | 1,966 | -0,287 | 1,551 | 1,937 |
| Wurf 2 | -0,262 | 1,369 | 1,969 | -0,262 | 1,420 | 1,898 |
| Wurf 3 | -0,296 | 1,523 | 1,936 | -0,343 | 1,578 | 1,969 |
| Wurf 4 | -0,295 | 1,517 | 1,937 | -0,264 | 1,463 | 1,919 |
| Wurf 5 | -0,287 | 1,538 | 1,898 | -0,303 | 1,523 | 1,936 |
| Wurf 6 | -0,297 | 1,551 | 1,919 | -0,296 | 1,538 | 1,966 |
| Wurf 7 | -0,343 | 1,691 | 2,084 | -0,291 | 1,691 | 2,017 |
| Wurf 8 | -0,291 | 1,463 | 2,017 | -0,313 | 1,534 | 1,973 |
| Wurf 9 | -0,264 | 1,420 | 1,973 | -0,295 | 1,369 | 2,084 |
| Wurf 10 | -0,313 | 1,578 | 2,066 | -0,297 | 1,517 | 2,066 |
Bei dem Permutationsverfahren werden für die Beschreibung der Flugkurven die gleichen Koeffizienten genutzt, allerdings werden diese nun zufällig kombiniert (siehe Tabelle 2, rechte Seite). Eine neue Flugkurve ergibt sich dann z. B. durch a0 aus Wurf 4, a1 aus Wurf 6 und a2 aus Wurf 5. Damit erhält man wieder 10 Flugkurven, bei denen die spezifischen Abstimmungen der Abwurfparameter innerhalb der Würfe aufgelöst wurden (vgl. Abbildung 14 B). Die Ergebnisvariabilität der neu berechneten Flugkurven beschreibt die aufgrund der Streuung der Ausführungsgrößen zu erwartende Ergebnisvariabilität (ErwEV) ohne Ausnutzung des Faktors Kovariation.
Durch die einmalige Anwendung des Permutationsverfahrens erhält man jedoch keine verlässliche Beschreibung der kovariationsbereinigten Ergebnisvariabilität. Auch bei zufälliger Kombination der Ausführungsgrößen können sich kompensierende oder verstärkende Passungen ergeben. Für eine exakte Bestimmung von ErwEV ist es erforderlich, die mittlere Streuung aller möglichen Kombinationen der Ausführungsgrößen zu ermitteln. Bei der Anwendung auf den dreidimensionalen Fall (5 Ausführungsgrößen) und 20 Würfen pro Bedingung sind dafür 205 = 3.200.000 Permutationsdurchgänge erforderlich. Aufgrund des hohen Rechenaufwandes beschränkt man sich in der Regel auf eine Schätzung des Mittelwertes aller möglichen Kombinationen aufgrund einer zufälligen Auswahl von Permutationen. Im vorliegenden Fall werden 5000 Wiederholungen des Verfahrens genutzt, wodurch eine hohe Genauigkeit der Schätzung erwartet werden kann.
Zu unterscheiden sind also die empirisch ermittelte Ergebnisvariabilität (EmpEV, hier 9.79 cm) der Originalflugkurven und die aufgrund der Ausführungsvariabilität zu erwartende Ergebnisvariabilität (ErwEV, hier 40.73 cm). Im vorliegenden Fall erhält man EmpEV < ErwEV. Dies zeigt, dass die Ausführungsgrößen systematisch so aufeinander abgestimmt werden, dass hohe Konstanz im Bewegungsergebnis resultiert. Aus den ermittelten Variabilitätswerten lässt sich nun durch Gleichung (1) (vgl. Abschnitt 4.2) der Kovariationskoeffizient R für multiple nicht-lineare Zusammenhänge bestimmen (Müller, 2001; Müller & Sternad, 2003). Negative Werte geben nun an, dass die Ausführungsgrößen systematisch so aufeinander abgestimmt sind, dass hohe Ergebniskonstanz resultiert. Anschaulich beschreibt der im vorliegenden Fall ermittelte Kovariationskoeffizient R = –.76, dass 76% der Ausführungsvariabilität durch Kovariation der Ausführungsparameter reduziert wurde.
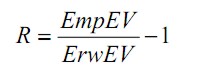 | (1) |
Für die gruppenstatistischen Betrachtungen wird der Kovariationskoeffizient R einer Fisher-Z-Transformation unterzogen.
5.3.8 Angaben zu den statistischen Analysen
Die inferenzstatistischen Analysen wurden mit den Statistikpaketen SPSS 12.0 und R 2.4.1 durchgeführt. An einigen Stellen wird dabei auf nicht-parametrische Verfahren für die Auswertung der vorliegenden zweifaktoriellen Versuchsanlage zurückgegriffen, die auf dem nicht-parametrischen Marginalmodell (Brunner & Langer, 1999; Brunner, Demhof & Langer, 2002) basieren.
Allgemein wird zur Ablehnung der Nullhypothese ein α-Fehler-Niveau von 5 % gewählt. Bei der Prüfung von Voraussetzungen, bei denen die Beibehaltung der Nullhypothese wünschenswert ist, wird ein α-Fehler-Niveau von 20 % genutzt. Ausreichende Varianzhomogenität wird mit dem Levene-Test überprüft. Die Testung der Normalverteilungsvoraussetzung erfolgt mit dem Kolmogoroff-Smirnov-Anpassungstest mit Lilliefors-Schranken, den Bortz, Lienert und Boehneke (1990, S. 319ff.) für kleine Stichproben empfehlen.
>> Ergebnisse