Psychischer Druck

Inhaltsverzeichnis der Doktorarbeit

Druck und Veränderungen der Bewegungsausführung

4.2 Faktoren der Trefferleistung

Die im letzten Abschnitt dargestellten Überlegungen und Ergebnisse deuten darauf hin, dass ein erneutes Einschränken von Freiheitsgraden die Abstimmung der Gelenkbewegungen beeinträchtigt und dies zu geringerer Konstanz im Endglied der Bewegung führt. Dabei bleibt jedoch unklar, wie sich diese Veränderungen auf das Bewegungsergebnis, also z. B. die Trefferleistung beim Freiwurf auswirkt. Im vorliegenden Abschnitt wird ein Konzept von Müller (2001; siehe auch Müller & Sternad, 2004) eingeführt, das diese Lücke für Aufgaben mit hohen Genauigkeits- und Konstanzleistungen schließt.

Viele sportliche Fertigkeiten erfordern hohe Präzisionsleistungen, die zudem sehr konstant hergestellt werden müssen. Betrachtet man z. B. den Basketball-Freiwurf, dann ergeben sich hohe Präzisionsanforderungen durch die Entfernung des Spielers zum Korb. Der Ring befindet sich in einer Höhe von 3.05 m und der Ringmittelpunkt ist 4.225 m von der Freiwurflinie entfernt. Der Durchmesser des Ringes beträgt 45 cm und der des Balles etwa 24 cm. Die Genauigkeitsanforderungen sind allerdings noch höher, wenn man den Eintrittswinkel des Balles in den Ring berücksichtigt. Der volle Korbdurchmesser steht für das Eintreten in den Korb nur dann zur Verfügung, wenn der Ball senkrecht von oben in den Ring eintritt. Beispielsweise beträgt die maximale Ausdehnung des Eintrittsbereichs in Wurfrichtung bei einem Eintrittswinkel von 45° nur noch etwa 32 cm. Für das Erzielen hoher Trefferquoten ist es zusätzlich erforderlich, dass die Flugkurven bei wiederholter Ausführung am Ring nur eine sehr geringe Streuung aufweisen.

Die Schwierigkeit bei der Realisierung der erforderlichen Genauigkeits- und Konstanzleistungen besteht darin, dass Bewegungsausführungen immer mit Ungenauigkeiten verbunden sind. Selbst nach sehr umfangreicher Übung können Bewegungen nicht in identischer Weise wiederholt werden (Bernstein, 1967; Newell & Corcos, 1993). Es stellt sich also die Frage, wie es trotz unvermeidbarer Ungenauigkeiten in der Bewegungsausführung gelingt, Bewegungsergebnisse sehr konstant herstellen zu können. Ein zentraler Aspekt stellt dabei die aufgabendienliche Kovariation von Ausführungsgrößen dar – Fluktuationen in einer Komponente werden durch Anpassungen in (einer) anderen ausgeglichen. Durch das von Müller (2001) eingeführte Konzept lassen sich insgesamt drei Faktoren unterscheiden, auf die Veränderungen der Ergebnisvariabilität vollständig zurückgeführt werden können. Hierdurch ergibt sich zum einen die Möglichkeit, übungsbedingte Veränderungen ergebnisrelevanter Größen zu beschreiben. Aber auch die Beeinflussung der Leistung etwa durch erhöhte Druckbedingungen lassen sich auf diese Ausführungsmerkmale zurückführen.

In Abbildung 8 (Reiser, 2004, S. 24) werden anhand einer Serie von Freiwürfen die Faktoren verdeutlicht, die prinzipiell zu einer Veränderung der Ergebnisvariabilität beitragen können². Genutzt wird dafür der Zusammenhang von Abwurfgeschwindigkeit und -winkel. Dargestellt sind zunächst alle Kombinationen, die zu einem Treffer (grau) bzw. zu einer Ringberührung (hellgrau) führen. Die einzelnen Punkte repräsentieren die Winkel-Geschwindigkeits-Kombinationen einer Serie von 10 Würfen, mit denen der Ball die Hand verlässt. Eine Wurfbewegung führt also dann zu einem Treffer, wenn der zugehörige Punkt innerhalb der grauen Treffermenge liegt. Es gibt drei Möglichkeiten die Trefferleistung einer Serie von Würfen zu verbessern. Die erste Möglichkeit besteht darin, die Stabilitätseigenschaften der Aufgabe optimal auszunutzen. In der Abbildung entspricht dies der Verschiebung der „Abwurf-Punktewolke“ in den Bereich, wo die graue Treffermenge am breitesten ist (Faktor „Stabilität des Abwurfbereichs“, Verschiebung von A nach B in Abbildung 8 a). Beim Freiwurf ist es z. B. aufgrund des oben dargestellten Zusammenhangs von Eintrittswinkel und Größe des Eintrittsbereichs günstig, eine hohe Flugkurve, also größere Abwurfwinkel zu wählen. Eine weitere Möglichkeit die Trefferleistung zu verbessern besteht darin, die Streuung der Ausführungsgrößen, also in diesem Beispiel von Abwurfwinkel und -geschwindigkeit zu verringern (Faktor „Größe der Streuung“). In Abbildung 8 b wird dies durch das Zusammenrücken der Punktewolke veranschaulicht. Schließlich besteht noch die Möglichkeit, die beiden Parameter so aufeinander abzustimmen, dass zu jedem Abwurfwinkel eine „passende“ Geschwindigkeit „gewählt“ wird, sodass deren Kombination zum Korberfolg führt (Faktor „aufgabendienliche Kovariation“). In Abbildung 8 c zeigt sich dies darin, dass die Form der Punktewolke auf die der Treffermenge angepasst wird.

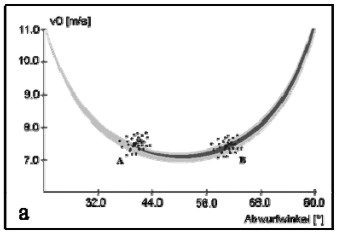
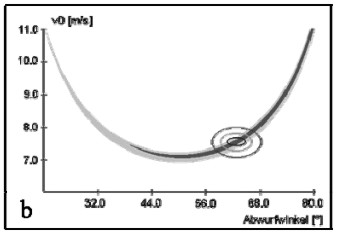
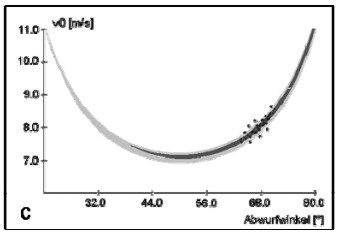
Abbildung 8 a-c: Treffermenge (grau, hellgrau Ringberührung) und hypothetische Abwurfmenge beim Basketball-Freiwurf (Reiser, 2004, S. 24). Veranschaulicht werden die Nutzung der Faktoren „Stabilität des Abwurfbereichs“ (a), „Größe der Streuung“ (b) und „aufgabendienliche Kovariation“ (c). Ausführliche Erläuterungen erfolgen im Text.

Untersuchungen anhand der Flugkurven beim Basketball-Freiwurf und beim Boule-Unterhandwurf zeigen erwartungsgemäß eine deutlich geringere Ergebnisvariabilität bei Experten als bei wenig geübten Personen (Reiser, Müller & Daugs, 1997a). Weiterhin kann durch aufgabendienliche Kovariation ein erheblicher Teil der Ausführungsvariabilität (60-80%) reduziert werden. Allerdings unterscheiden sich Experten und Novizen in der Nutzung dieses Faktors nur in geringem Maße. Dies deutet darauf hin, dass durch die Nutzung der freiwurftypischen Bewegungstechnik – selbst bei wenig geübten Spielern – schon ein hohes Maß an Kovariation von Abwurfwinkeln und -geschwindigkeiten sicherstellt wird. Dagegen ist bei den Experten eine deutlich geringe Variabilität in den Abwurfparametern zu finden, was ebenfalls zu einer geringen Streuung der Flugkurven am Ring beiträgt. Dies könnte wiederum auf eine stärkere Nutzung aufgabendienlicher Kovariation auf Gelenkebene im Sinne einer hohen Konstanz im Endglied der Bewegung hindeuten, wie dies die Ergebnisse von Hossner (2004) bzw. McDonald et al. (1989) nahe legen.

Entsprechend dieser Erwartung zeigt sich aufgabendienliche Kovariation bei ganz verschiedenen Fertigkeiten und auf unterschiedlichen Ebenen der Ausführung. Eine ausführliche Zusammenstellung von Arbeiten zur Nutzung aufgabendienlicher Kovariation ist bei Müller (2001) zu finden. Im Folgenden werden beispielhaft einige Arbeiten aufgeführt, die verdeutlichen sollen, dass aufgabendienliche Kovariation auf ganz unterschiedlichen Ebenen zu beobachten ist. So kann Bootsma (1988) Kovariation temporaler Parameter bei Schlagbewegungen im Tischtennis nachweisen. Schlagdauer und Bewegungsbeginn werden so aufeinander abgestimmt, dass hohe Konstanz im Treffpunkt des Balles resultiert. Wie bereits beschrieben zeigen sich bei Hossner (2004) posturale Kompensationseffekte bei der Analyse der Körperhaltung bei der Basketball-Freiwurfbewegung. Basketball-Experten stimmen ihre Gelenkbewegungen so aufeinander ab, dass geringe Streuungen im Endpunkt der Bewegungskette entstehen. Eine Reihe von Untersuchungen von Zielwürfen finden Kovariation der Abwurfparameter des Wurfobjektes, sodass eine geringe Streuung im Ziel resultiert (Reiser et al., 1997a, 1997b; Müller & Loosch, 1999; Reiser, 2004).

Die dargestellten Ergebnisse zur Nutzung aufgabendienlicher Kovariation führen zu der Frage, wie diese Abstimmungen im Ausführungsprozess erzielt werden können. Wurf-, Stoß- und Schlagbewegungen sind von sehr kurzer Dauer. Aufgrund der zeitlichen Einschränkungen der menschlichen Informationsverarbeitung können die kompensatorischen Prozesse nicht oder zumindest nicht vollständig durch die Verarbeitung proprio- und exterozeptiver Rückmeldungen erklärt werden (vgl. Müller, 2001; Reiser, 2004). Reiser (2004) kann zeigen, dass im Lernverlauf zunehmend äquifinale Bewegungsabschnitte im Abwurfbereich realisiert werden. Darunter ist zu verstehen, dass über einen Bewegungsabschnitt nur solche Kombinationen von Abwurfwinkeln und -geschwindigkeiten vorliegen, die zum Ziel führen. Anschaulich würde dies in Abbildung 8 bedeuten, dass die bei der Bewegungsausführung realisierten Winkel-Geschwindigkeits-Kombinationen im Abwurfbereich in der grauen Treffermenge verlaufen und diese nicht nur kurz schneiden. Trotz nicht vermeidbarer Streuungen des Abwurfzeitpunktes und der Abwurfparameter kann so das Ziel mit hoher Sicherheit erreicht werden. Verlässt der Ball in einem solchen äquifinalen Bewegungsabschnitt die Hand, dann impliziert dies die hohe Abstimmung der Abwurfparameter. Dies liefert eine Erklärung dafür, wie bei Zielwürfen ein hohes Maß aufgabendienlicher Kovariation der Abwurfparameter realisiert werden kann und hierdurch eine geringe Ergebnisvariabilität resultiert.

Damit ist es möglich, dass sich die Abnahme kompensatorischer Abstimmungen auf Gelenkebene gleich in zweifacher Hinsicht negativ auf den resultierenden Ballflug auswirkt. Zum einen sollten größere Streuungen der Abwurfparameter resultieren und zum anderen könnte es weniger gut gelingen, äquifinale Bewegungsbahnen anzusteuern und damit Kovariation der Abwurfparameter zu nutzen.

Für die Quantifizierung aufgabendienlicher Kovariation ist es erforderlich, die Aufgabe mathematisch zu modellieren, d. h. aus den Ausführungsgrößen das Bewegungsergebnis berechnen zu können. Aus diesem Grund eignen sich Wurf-, Schuss- oder Schlagbewegungen für entsprechende Berechnungen. Die Bewegungsausführung resultiert in der Flugbahn eines Objektes, die anhand des schiefen Wurfs gut beschrieben werden kann. Damit ist es möglich, aus den Ausführungsgrößen das Bewegungsergebnis zu bestimmen und die empirisch gefundene Ergebnisvariabilität (EmpEV) für wiederholte Ausführungen zu ermitteln. Durch ein von Müller (2001; Müller & Sternad, 2003) vorgeschlagenes Permutationsverfahren können die spezifischen Kopplungen innerhalb einer Serie von Ausführungen aufgelöst werden. Hierdurch wird es möglich, die aufgrund der Streuung der Ausführungsgrößen theoretisch zu erwartende Ergebnisvariabilität (Erw-EV) ohne Ausnutzung des Faktors Kovariation zu bestimmen. Damit kann durch Gleichung (1) Kovariation für multiple nicht-lineare Zusammenhänge berechnet werden (Müller, 2001; Müller & Sternad, 2003).

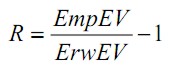
Mithilfe des dargestellten Vorgehens lässt sich also bestimmen, wie sich Veränderungen auf der Ausführungsebene (z. B. Abwurfwinkel, -geschwindigkeit und -höhe) auf der Ergebnisebene (z. B. die Streuung der Flugkurven am Korb) auswirken. Anhand der Flugkurven wird zwar keine direkte Betrachtung der Bewegungsausführung vorgenommen, allerdings stellen sie die ergebnisrelevante Summe der vorausgegangenen Körperbewegungen dar (Müller, 2001, S. 114). Die Übertragung der Überlegungen auf die Koordination der Gelenke erfordert bei Ganzkörperbewegungen eine äußerst komplexe Modellierung.

Die kovariationsbereinigte, theoretisch zu erwartende Ergebnisvariabilität (ErwEV) stellt ein Maß zur Beschreibung der Ausführungsvariabilität dar. Der verallgemeinerte Kovariationskoeffizient R quantifiziert aufgabendienliche Kovariation auch für multiple nicht-lineare Zusammenhänge.

² An dieser Stelle handelt es sich aus Gründen der Anschaulichkeit um eine vereinfachte Darstellung. Dabei wird der Ballflug lediglich zweidimensional und bei festem Abwurfpunkt betrachtet. Die Zusammenhänge und Berechnungen sind aber nicht auf diesen Fall beschränkt.

>> Studien zur Veränderung des Bewegungsverhaltens in Drucksituationen