Zur Anordnung der Zahlen auf dem Dartboard

Die Frage ist so alt wie die Scheibe: »Warum sind die Zahlen auf dem Dartboard so angeordnet?« Die üblichen Antworten sind unbefriedigend. Große Zahlen stünden neben kleinen (was nicht falsch ist; ginge es aber nur darum, gäbe es 660 Milliarden bessere Lösungen – dazu gleich), meistens wird auf die Entstehungsgeschichte verwiesen, wie Brian Gamlin anno 1896 diese Anordnung erfand – eine gute Antwort auf die Frage »Wie kam es dazu?«, aber keine nach dem Warum.

Ein System, das sich seit 120 Jahren bewährt hat, das nie ernsthaft bezweifelt wurde, dem bis vor kurzem keine auch nur ansatzweise haltbare Alternative gegenüberstand – so ein System muss eine innere Logik besitzen, muss »in sich stimmen«, muss bestimmten mathematischen Gesetzen folgen. Diese innere Logik soll hier untersucht und aufgezeigt werden.

Versucht wurde der Kompromiss, Allgemeinverständlichkeit mit mathematischer Genauigkeit zu vereinen. Kundige der Mathematik mögen also Umständlichkeiten und kleine Vereinfachungen verzeihen, in dieser Sprache weniger Bewanderte manch Mühe beim Nachvollziehen der Gedankengänge. Für das Gesamtverständnis nicht unbedingt notwendige Informationen, wie Präzisierungen oder Formeln, wurden in Kästchen ausgelagert.

Zunächst ein paar Worte zur ungeheueren Menge aller möglichen Anordnungen.

Die Zahlen von 1 bis 20 kreisförmig anzuordnen gibt es 19! Möglichkeiten. Schließt man sinnvollerweise drehrichtungssymmetrische Lösungen aus (also im oder gegen den Uhrzeigersinn gelesen gleiche), bleiben 19!/2 = 60.822.550.204.416.000 Möglichkeiten übrig, in Worten gut 60,8 Billiarden. Um eine kleine Vorstellung von dieser Zahl zu bekommen: würde man jede Sekunde 1000 Anordnungen ausprobieren, wäre man fast 2 Millionen Jahre beschäftigt.

Das Ziel ist offenbar, auf dem Board ein größtmögliches Chaos anzurichten, d.h. die Zahlen so ungeordnet wie möglich zu verteilen. Das Problem ist schwieriger als gedacht. Es wurde von zwei Seiten angegangen: zum einen »bottom-up«, von wenigen Feldern ausgehend, wo die Zahl der Anordnungen und Ergebnisse noch überschaubar ist, zum anderen »top-down«, auf dem Standardboard (StaB) Prinzipien zu finden, die dann auf »Boards« mit weniger als 20 Feldern überprüft wurden.

Die Anzahl der Felder (gleich der größten Zahl) wird im weiteren mit n bezeichnet. Es stellt sich schnell heraus, dass ungeradzahlige n Ergebnisse liefern, die mit dem StaB nicht vergleichbar sind (und alle Formeln schrecklich verkomplizieren würden!). Zunächst ist n also eine gerade Zahl, später kommt eine weitere Einschränkung dazu. Und damit – auf in die Tiefen des Chaos!

Voraussetzung

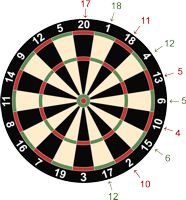
Neben der 20 steht die 1.

Das Axiom des Dartboards, mathematisch nicht begründ- und herleitbar: die pure Boshaftigkeit.

Bis n = 10 wurden alle Anordnungen hinsichtlich des größtmöglichen Chaos untersucht, auf Dutzende verschiedener Methoden, doch wie immer sie auch durchforstet wurden: nie ergab sich eine Lösung, bei der die höchste Zahl neben der 1 stand. Offensichtlich soll auf diese »Gemeinheit« nicht verzichtet werden – selbst auf Kosten einer maximalen Unordnung.

Nach dieser Erkenntnis wurden nur noch Anordnungen unter dieser Voraussetzung untersucht, für alle folgenden Angaben gilt somit:

Die Anzahl der Anordnungen für n = 20 reduziert sich damit von 19!/2 auf 18!, das sind rund 6,4 Billiarden.

Kriterium 1

Das erste und wichtigste Kriterium ist tatsächlich eine möglichst große Differenz der Zahlen benachbarter Felder. Beim StaB mit 20, 1, 18, 4, 13, 6, ... erhält man 19, 17, 14, 9, 7, ... Die Summe dieser Differenzen sei S genannt.

Der Minimalwert S_min = 38 ist leicht zu finden, etwa bei der größtmöglichen Ordnung 1, 2, 3, ..., 20 oder der für den Dartspieler wohl »günstigsten« Variante 20, 18, 16, ..., 4, 2, 1, 3, 5, ..., 17, 19.

Das Maximum S_max beträgt 200, auch dafür lässt sich leicht eine Lösung finden.

Alle geradzahligen Werte zwischen S_min und S_max sind möglich. Das StaB liefert S = 198. Warum gab sich Mr. Gamlin mit der zweitbesten Lösung zufrieden? Sollte er die Maximallösung einfach übersehen haben?

Natürlich nicht, ein guter Zimmermann übersieht nichts. Die maximale Summe ist eben nicht die optimale Lösung.

S_max ist nur erreichbar mit dem »sturen« Wechsel zwischen hoch und tief. Alle Zahlen über 10 lägen auf Schwarz, alle kleinen auf Weiß (oder umgekehrt). Das aber stellt wieder eine Ordnung dar und widerspricht damit dem Ziel des größtmöglichen Chaos. An zwei Stellen ist deshalb der Wechsel hoch/tief unterbrochen: 6, 10, 15 und 8, 11, 14.

	n=20	Anzahl der möglichen Anordnungen	Anzahl für n=20
Smin = 2(n – 1)	38	2n–3	132.072
Smax = 2(n/2)2	200	n(n/2 – 1)!2 / 4	rd. 660 Mrd.
Smax – 2	198	[ 2(n – 3)(n/2 – 1)! / (n – 2) ]2	rd. 470 Mrd.

Das 1. Kriterium ist also: die Summe der (absoluten) Differenzen aller benachbarten Zahlen hat den zweithöchsten Wert, kurz

Kriterium 2

Auf der Dartscheibe fallen nicht nur die großen Differenzen benachbarter, sondern auch die gegenüberliegender Zahlen auf: 17, 18, 11, 12, 5, ... Ihre Summe sei T genannt.

Nach einer halben »Runde« kommt wieder das erste Zahlenpaar, es gibt also nur halb so viele Summanden wie bei S. Auch der Maximalwert ist halb so groß, nämlich 100, etwa wenn sich alle gegenüberliegenden Zahlen um 10 unterscheiden. Die jeweilige Differenz 1 ergibt den Minimalwert 10.

	n=20	Anzahl der möglichen Anordnungen	Anzahl für n=20
Tmin = n/2	10	2n/2–2 * (n/2 – 2)!	10.321.920
Tmax = (n/2)2	100	2n/2–2 * (n/2 – 1)!2	rd. 34 Bio.

Nun ist T_StaB = T_max. Bei n = 20 liefert durchschnittlich nur 1 von 190 Anordnungen T_max – offensichtlich steckt Absicht dahinter.

Das 2. Kriterium lautet also

Die beiden Kriterien haben einen verblüffenden Effekt. So oft sie bei allen n auch vorkommen mögen – zusammen treten sie nur bei n auf, die Vielfache von 4 sind.

Für die weiteren Untersuchungen standen damit zur Verfügung:

n =  4	1 (triviale) Lösung
n =  8	32 Lösungen
n = 12	9.216 Lösungen
n = 16	12.441.600 Lösungen

Für n = 20 gibt es vermutlich 43.104.337.920 Lösungen, die endgültige Überprüfung bliebe auf jeden Fall einem Großrechner vorbehalten.

Aus den gegebenen Lösungen soll nun das Prinzip gefunden werden, nach dem das StaB aufgebaut ist, mit dem –

Kriterium 3

Bei ihm wird es ein wenig schwieriger. Zum einen was die Darstellung betrifft – keine Bange, es wird Schritt für Schritt erklärt –, zum anderen die unmittelbare Einsichtigkeit. Die Voraussetzung und das 1. Kriterium erklären sich von selbst, das 2. bei näherem Hinsehen auch, dieses 3., so zwingend es am Ende erscheinen mag, behält einen Hauch von Geheimnis.

Gehn wir’s an.

1. Die Summen

Bisher ging es um Differenzen, einmal benachbarter, andermal gegenüberliegender Zahlen. Jetzt geht es um Summen.

Von jedem Feld aus werden alle sinnvollen Summen R mit p Summanden im Abstand q gebildet. Für jedes p und jedes q erhält man also n Werte: R(1)_p,q, R(2)_p,q, ..., R(n)_p,q, im weiteren als R_p,q zusammengefasst.

An einem Beispiel soll das veranschaulicht werden, der Einfachheit halber für n = 8.

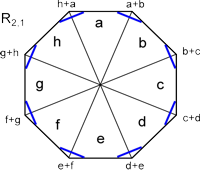
Die erste Folge von Summen ist R_2,1,, es werden je 2 Zahlen im Abstand 1 zusammengezählt: a+b, b+c, c+d, ..., h+a.

Es geht weiter mit R_2,2, 2 Summanden im Abstand 2, also a+c, b+d, c+e, ..., h+b. Dann R_2,3 mit a+d, b+e, ..., h+c, usw. R_4,3, um ein letztes Bespiel zu geben, liefert a+d+g+b, b+e+h+c, ... – und so weiter und so fort, bis –

– tja, bis wohin? Die Definition der »sinnvollen Summen« lässt sich nicht mehr umgehen. Bei q geht das noch recht leicht: der kleinste Abstand ist natürlich 1, und ab q > n/2 wiederholen sich die Ergebnisse. So ergeben sich etwa (immer noch Bsp. n = 8) für R_2,5 die gleichen Zahlen wie für R_2,3, nur in anderer Reihenfolge.

Auch q = n/2 liefert irrelevante Werte, es würden nur gegenüberliegende Zahlen immer wieder zusammengezählt. Für q gilt also: 1 ≤ q ≤ n/2 – 1.

Deutlich schwieriger ist es mit der Anzahl der Summanden p. Um die Sache nicht unnötig zu komplizieren und in die Länge zu ziehen, sei hier nur das nach reiflicher Überlegung als sinnvoll erachtete Ergebnis angegeben: 2 Summanden müssen es mindestens sein, mehr als n/2 bringen keinen wesentlichen Erkenntnisgewinn. Somit: 2 ≤ p ≤ n/2.

Man hat nun also für n = 20 insgesamt 9*9 = 81 Zahlenreihen R_p,q mit je 20 Werten:

R_2,1, R_2,2, ..., R_2,9
R_3,1, R_3,2, ..., R_3,9
.
.
.
R_10,1, R_10,2, ..., R_10,9

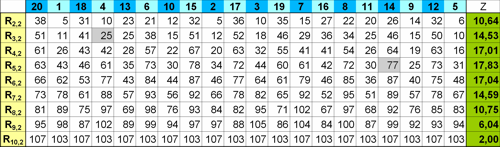
Von jedem R_p,q wird nun die Standardabweichung Z berechnet. Die Standardabweichung ist ein übliches Maß in der Statistik; sie gibt an, wie weit die einzelnen Werte um den Mittelwert streuen.

Als Beispiel die Werte R_p,2 und ihre Z, die sich auf dem StaB (blau unterlegt) ergeben. Links steht, was in der Zeile berechnet wird (2 bis 10 Summanden im Abstand 2). Die beiden grau markierten Werte etwa setzen sich so zusammen: die 25 (3 Summanden, Abst. 2) aus 4 + 6 + 15, die 77 (5 Summanden, Abst. 2) aus 14 + 12 + 20 + 18 + 13. Grün unterlegt dann die Standardabweichung der jeweiligen Zeile.

Tabelle Z

Soweit alles klar? Keine ganz leichte Kost, aber hoffentlich verständlich genug erklärt. Was soll damit aber nun gewonnen sein?

2. MiniMax

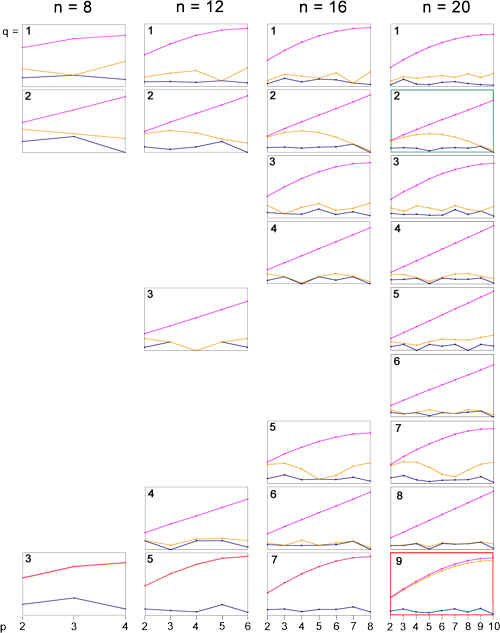
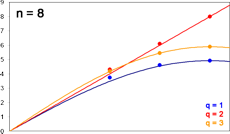
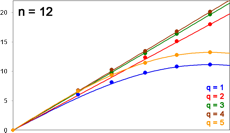
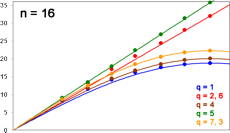
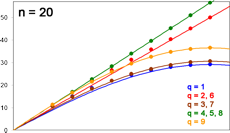
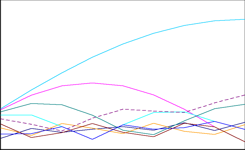
Betrachten wir die folgende Grafik. Für alle relevanten n und q sind ausgewählte Werte Z in Abhängigkeit von p darstellt, kurz: Z als Funktion von p.

Auf den blauen Kurven liegen die minimalen, auf den violetten die maximalen Werte von Z, für n = 8 und 12 von allen Anordnungen, für n = 16 und 20 von je rund 20.000 Zufallsanordnungen (plus einigen sorgsam konstruierten Anordnungen – hervorragende Min-/Max-Lieferanten!). Für diese Werte gilt die Voraussetzung (neben n steht die 1), nicht aber das 1. und 2. Kriterium.

Zu den gelben Kurven später, die scheinbar roten in der unteren Zeile sind Überlagerungen von violett und gelb.

Die Ähnlichkeit der Kurvenverläufe in jeder Zeile fällt ins Auge. Ganz offensichtlich sind die Ergebnisse für alle n vergleichbar.

Abbildung Z

3. Ein Sinus schwingt durchs Board

Die (blauen) min-Werte wackeln etwas ziellos durch die Gegend, um so erstaunlicher die (violetten) max-Werte: es sind entweder (fast) genaue Geraden oder (fast) genaue Sinuskurven. Die endgültige Formulierung des 3. Kriteriums wird damit sehr vereinfacht, wie sich zeigen wird.

Es ist immer wieder verblüffend, wie oft man in den unterschiedlichsten Zusammenhängen, plötzlich und unerwartet, auf den Sinus stößt. Man zählt nichtsahnend ein, zwei Handvoll Zahlen auf dem Dartboard zusammen, schaut nach, wie die Ergebnisse voneinander abweichen, und zack – ein Sinus. Die wunderbare Welt der Mathematik ...

Für Interessierte folgen hier einige nähere Angaben zu diesen Maxima, die für das Gesamtverständnis nicht notwendig sind. Wem schon der Kopf rauchen sollte, lese getrost bei 4. weiter.

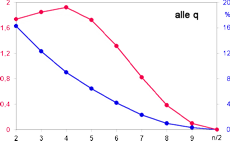
Graphen sagen mehr als tausend Worte, deshalb hier zusammengefasst nochmals die Maxima aus Abb. Z. Bei n = 16 und 20 fallen einige Graphen nahezu zusammen.

Den Graphen liegen folgende Funktionen zugrunde:
f(Z) = 2p/n * Z_n/2,q für die Geraden,
f(Z) = sin(p*pi/n) * Z_n/2,q für die Sinuskurven.

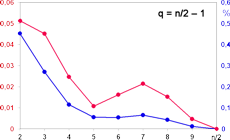
Die Punkte sind die jeweiligen tatsächlichen Werte. Man sieht die stupend genaue Übereinstimmung, nur bei kleinen p weichen sie leicht nach oben ab. Hier die größten absoluten (rot) und relativen (blau) Abweichungen in Abhängigkeit von p.

4. Der rote Kasten – ein Ergebnis

Kommen wir zu den gelben Kurven in Abb. Z. Für n = 20 liegt ja ein festes Ergebnis vor, nämlich der Untersuchungsgegenstand: das StaB – und genau dessen Z-Werte sind hier aufgetragen; im grün eingefassten Kasten (n = 20, q = 2) sind das also die Z-Werte aus Tab. Z.

Die meisten realen Werte liegen in der Nähe der Minimalwerte, mit einer sehr aus dem Rahmen fallenden Ausnahme: Z_p,9, der rot eingefasste Kasten.

Nirgends sonst liegen die realen Werte so nahe bei einer der min-/max-Kurven. Offensichtlich handelt es sich bei den Maximalwerten für Z_p,9 (allgemein für Z_p,n/2–1) um das 3. Kriterium. Nun bilden diese Werte, wie oben gezeigt, eine nahezu perfekte Sinuskurve (mit einer maximalen Abweichung von weniger als 0,5 %), d.h. es genügt die Auswahl eines einzigen Wertes, die anderen ergeben sich mit hinreichender Genauigkeit aus der o.a. Sinusfunktion. Bei Z_10,9 (allgem. Z_n/2,n/2–1, im weiteren Z_rot) ist der Fehler am kleinsten, tatsächlich ist es aber belanglos, ob alle Z_p,n/2–1 verwendet werden oder nur Z_rot, man erhält dieselben Lösungen. Die gelben Punkte bei n = 8, 12 und 16 in Abb. Z sind die Z-Werte der Lösungen, die sich aus den drei Kriterien ergeben. Weiter unten wird darauf eingegangen.

Als 3. Kriterium kann also formuliert werden:

– das allerdings einen Haken hat: es wird bei Anwendung auf n = 20 nicht das StaB liefern. Bei ihm ist Z_rot = 34,841, eine andere Lösung (auch dazu weiter unten) kommt auf 36,617 (möglicherweise das absolute Maximum).

Wieder scheint Gamlins Lösung suboptimal zu sein, und wieder ist sie es nicht, zumindest nicht aus seiner Zeit und Sicht.

Zu Gamlins Zeiten war die übliche Spielregel, die Zahlen der Reihe nach von 1 bis 20 abzuschießen. Angrenzende Nachbarzahlen hätten das Spiel erleichtert – das wollte tunlichst vermieden werden. Bei allen (bekannten) Anordnungen mit größerem Z_rot treten aber genau die auf.

Für das StaB gilt also eine zweite Voraussetzung, die mit den heute weltweit üblichen Spielregeln obsolet geworden ist: Nachbarzahlen liegen nicht auf Nachbarfeldern.

Zusammenfassung

Das Standardboard ist nach folgenden Prinzipien aufgebaut:

• neben der 20 steht die 1
• benachbarte Zahlen liegen nicht auf benachbarten Feldern
• die Summe S der (absoluten) Differenzen aller benachbarten Felder hat den zweithöchsten möglichen Wert 198
• die Summe T der (absoluten) Differenzen aller gegenüberliegenden Felder hat den höchstmöglichen Wert 100
• wird von jedem Feld aus eine Summe aus 10 Summanden gebildet, die im Uhrzeigersinn jeweils den Abstand von 9 Feldern haben, hat die Standardabweichung Z_rot dieser Summen den höchstmöglichen Wert

Einige Anordnungen im Vergleich

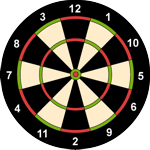
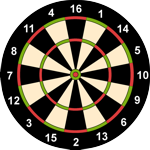
Zunächst seien die Lösungen für n = 8, 12 und 16 angegeben, die sich bei strikter Anwendung der drei Kriterien ergeben (im weiteren K-Boards genannt).

Einige Ähnlichkeiten mit dem StaB sind unverkennbar:

• n – 1 (die zweitgrößte Zahl) gegenüber der 1
• n – 2 rechts der 1
• n – 3 gegenüber dem Feld links von n

Das Ergebnis für n = 16 zu ermitteln ging an die Grenzen eines PC. Ein kleines Programm (in Python, Dank an Jakob Kunzmann) siebte zunächst – in ca. 40 Stunden Laufzeit – aus 50 Milliarden Möglichkeiten die 12,4 Millionen mit passendem S und T aus, die zu weiteren Berechnungen auf 24 Excel-Dateien verteilt wurden. Um auch für n = 20 ein Ergebnis liefern zu können, wurden die eben genannten Punkte vorausgesetzt, dazu eine weitere Gemeinsamkeit der Lösungen für n = 8, 12 und 16, nämlich: gegenüber n liegt die 2.

Die untersuchten Anordnungen hatten somit die Form:

20, 1, 18, x₄, x₅, x₆, x₇, x₈, x₉, 17, 2, 19, x₁₃, x₁₄, x₁₅, x₁₆, x₁₇, x₁₈, x₁₉, x₂₀

Für x₂₀ kommen nur die Werte 3 ... 11 in Frage (die Gründe dafür zu erläutern würde diesen Rahmen sprengen). Damit war der Aufwand mit dem für n = 16 zu vergleichen und also machbar. Ob das Ergebnis tatsächlich das gesuchte K-Board ist, ist wegen der Vorbedingungen nicht gesichert; einige wichtige Gründe sprechen aber dafür.

Vor dem Vergleich mit dem StaB sei noch das »Optimal Dartboard« erwähnt, das von dem Mathematikprofessor David Percy 2013 bei der BDO Weltmeisterschaft vorgestellt wurde. Kriterium 1 (S = 198) gilt auch bei ihm, mit der gleichen Begründung wie im entsprechenden Kapitel oben. Kriterium 3 fließt anders, aber vergleichbar ein. Kriterium 2 unterscheidet sich grundsätzlich: beim K-Board T = T_max, bei Percy der stete Wechsel von geraden und ungeraden Zahlen.

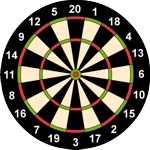
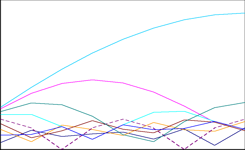
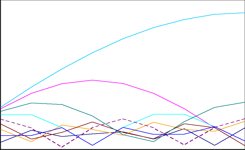
Hier die drei Scheiben im Vergleich, daneben ihre Z-Werte.

Gamlin’s Board

Percy’s Board

K-Board

Zunächst erstaunt bei den Neuordnungen, dass weitgehend unterschiedliche Ansätze ein fast gleiches Ergebnis liefern: 12 Zahlen an der gleichen Stelle, die übrigen 8 gespiegelt (die nahezu gleichen Z-Werte ergeben sich damit zwangsläufig). Erstaunlicher noch ist deren Ähnlichkeit mit Gamlin’s Board. S = 198 war jeweils Konstruktionsprinzip, beim K-Board auch T = 100 (bemerkenswert ist, dass sich das bei Percy quasi »nebenbei« ergeben hat), darüberhinaus stehen acht bzw. sieben Zahlen an der gleichen Stelle, die Kurven der Z verlaufen »parallel«, streckenweise gar deckungsgleich. Lediglich bei Z_p,5 (gestrichelte Linie) weicht das StaB deutlich von den neuen Lösungen ab.

Zu ergänzen sind noch die Werte für Z_rot:

34,841 (Gamlin)
36,513 (Percy)
36,617 (K)

Eine Wertung, welche Anordnung nun »besser« oder »schlechter« ist, ist nicht Thema dieses Artikels. Ein paar kleine Bemerkungen seien aber gemacht.

Das erklärte Ziel der Zahlenanordungen, auf allen Boards, ist, »Glückstreffer« zu vermeiden, es dem Spieler also so schwer wie möglich zu machen. Zu Gamlins Zeiten, mit den damaligen Spielregeln, war es durchaus sinnvoll, Nachbarzahlen auf Nachbarfeldern zu vermeiden. Diese Vorgabe ist nach den heutigen Regeln obsolet geworden.

Diese Regeln, vor allem die des üblichen »double out«, legen auch das größte Manko des StaBs offen, auf das auch Percy ausdrücklich hinweist: die Nachbarfelder 16 und 8 – beim Ausschießen ist das eine deutliche Erleichterung.

Ist es Zeit für eine neue Scheibe? »Tradition ist Schlamperei«, meinte Gustav Mahler, aber sie hat ein gewaltiges Gewicht. In Old England, der Heimat des modernen Dartsports, wohl noch mehr als anderswo.

Abschließend sei noch auf eine Kuriosität hingewiesen, auf die ich im Zuge dieser Arbeit stieß: das »Manchester Board«. Die Analyse dieser Simplizität wäre auf einer Seite erledigt gewesen. Was für den genialen Wurf Mr. Gamlins, auf den kleinsten Gedanken reduziert, stereotyp behauptet wird – große Zahlen lägen neben kleinen –, trifft hier zu. S = S_max = 200, groß neben klein eben. Sonst: nichts. NICHTS! Absolutely nothing! (Ok: nearly nothing.)

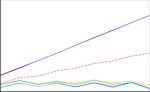
Die Z-Werte zeigen es – welch trübsinnige Ödnis und uninspirierte Langeweile hier, welch wunderbar chaotische Ordnung, welch großartig organisiertes Chaos bei Gamlin!

Hommage á Gamlin

Wenn ich in meinem Bekanntenkreis erzählte, womit ich mich aktuell beschäftige, kam immer die gleiche Reaktion: »Hatte dieser Gamlin nicht einfach rumprobiert?« Mich erinnert das an Äußerungen zu Bildern von Picasso (oder Klee oder Miró oder wem auch immer): »Das kann mein sechsjähriges Kind auch.«

Nun – nein, kann es nicht, und nein, Mr. Gamlin hat nicht einfach probiert. Im Lauf dieser Arbeit stieg meine Hochachtung vor diesem Zimmermann immer mehr, vor seinem »Gefühl«, seinem tatsächlichen wie intuitiven Verständnis für Zahlen.

S_max – 2 und T_max waren ohne jeden Zweifel gewollt und konstruiert, mit einfachem Herumprobieren ist das nicht zu erreichen. Kenntnis von Standardabweichungen hatte Gamlin vermutlich nicht – umso bewundernswerter, dass er eine Lösung fand, deren Z_p,9 nicht nur eine fast perfekte Sinuskurve ergeben, was allein schon selten genug vorkommt, sondern auch sehr nahe bei den maximalen Werten liegen. Eine Anordnung, ausgewählt aus, es sei nochmals erwähnt: 6,4 Billiarden!

Percy und ich gingen das Problem mit in einem Fall großem, im andern durchschnittlichem mathematischem Fachwissen an, uns stand die Leistungsfähigkeit moderner Rechenmaschinen zur Verfügung.

Gamlin war Zimmermann, ihm standen Stift und Papier, ein untrügliches Gespür für Zahlen und eine unerschöpfliche Geduld zur Verfügung. Er kam, mehr als ein Jahrhundert vorher, zu einem frappierend ähnlichen Ergebnis.

Wurde Brian Gamlin eigentlich irgendwo ein Denkmal errichtet?

Jochen Kunzmann